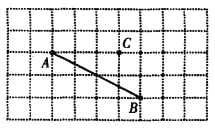
��Ŀ����
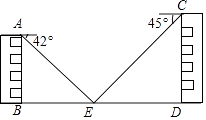
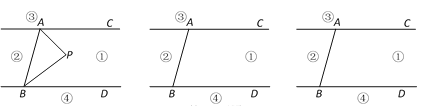
����Ŀ����ͼ��ֱ��AC��BD������AB��ֱ��AC��BD���߶�AB��ƽ��ֳɢ١��ڡ��ۡ����ĸ����֣��涨�����ϸ��㲻�����κβ��֣�������P����ij������ʱ������PA��PB�����ɡ�PAC����APB����PBD�����ǣ�(��ʾ���й����˵�������غϵ���������ɵĽ���0��)
(1)������P���ڵڢٲ���ʱ���С�APB����PAC����PBD����˵�����ɣ�
(2)������P���ڵڢڲ���ʱ����APB����PAC����PBD�Ƿ������������������д����PAC����APB����PBD�����ǵĵ�����ϵ(����˵������)��
(3)������P�ڵڢ۲���ʱ��̽����PAC����APB����PBD֮��Ĺ�ϵ��д���㷢�ֵ�һ������������˵����
���𰸡��Ƕȱ任���ڽǵĺ͵Ȼ���֪ʶת������2��![]() ��3����PBD����APB����PAC
��3����PBD����APB����PAC
��������
���⣨1��![]() 1��
1��
����P��PE//AC 1��
����PE//BD
����![]() ��
��![]() 3��
3��
����![]() 4��
4��
(2) ������ 5��
![]() 7��
7��
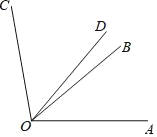
��3������P��ֱ��AB��࣬����PAC����APB����PBD�� 8��
����P��ֱ��AB�Ҳ࣬����PBD����APB����PAC 9��

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ