题目内容
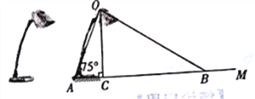
【题目】如图,点O为直线AB上一点,过点O作直线OC,已知∠AOC≠90°,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE.

(1)求∠DOE和∠DOF的度数;
(2)若∠DOC=3∠COF,求∠AOC的度数;
(3)求∠BOF+∠DOC的度数.
【答案】(1)∠DOE=90°,∠DOF=45°;(2)∠AOC=67.5° ;(3)∠BOF+∠DOC=135°
【解析】
(1)根据 射线OD平分∠AOC,射线OE平分∠BOC,即可求出∠DOE,再根据OF平分∠DOE,即可求出∠DOF的度数;
(2),由∠DOC=3∠COF,得出∠DOC的度数,再根据OD平分∠AOC,即可求得∠AOC的度数.
(3)先根据射线OD平分∠AOC,∠AOD=∠COD,得到,![]() ,再根据∠AOC+∠BOC=180°,得出∠DOE=90°,由射线OF平分∠DOE,得∠DOF=∠EOF=45°,从而求得∠FOB+∠DOC的度数;
,再根据∠AOC+∠BOC=180°,得出∠DOE=90°,由射线OF平分∠DOE,得∠DOF=∠EOF=45°,从而求得∠FOB+∠DOC的度数;
(1)![]() ,
,
![]()
∴![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() .
.
(2)∵∠DOC=3∠COF,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵OD平分∠AOC,
∴![]() .
.
(3)∵OD平分∠AOC,∴![]() ,
,
∴![]()
=![]() .
.

练习册系列答案
相关题目