题目内容
【题目】关于三角函数有如下的公式:
sin(α+β)=sinαcosβ+cosαsinβ①
cos(α+β)=cosαcosβ﹣sinαsinβ②
tan(α+β)=![]() ③
③
利用这些公式可将某些不是特殊角的三角函数转化为特殊角的三角函数来求值,如:
tan105°=tan(45°+60°)=![]() =﹣(2+
=﹣(2+![]() ).
).
根据上面的知识,你可以选择适当的公式解决下面的实际问题:
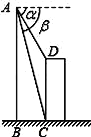
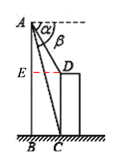
如图,直升飞机在一建筑物CD上方A点处测得建筑物顶端D点的俯角α=60°,底端C点的俯角β=75°,此时直升飞机与建筑物CD的水平距离BC为42m,求建筑物CD的高.
【答案】84米
【解析】分析:
如图,过点D作DE⊥AB于点E,由题意易得∠ACB=75°,∠ABC=90°,DE=BC=42m,∠ADE=60°,这样在Rt△ABC和在Rt△ADE中,结合题中所给关系式分别求出AB和AE的长,即可由CD=BE=AB-AE求得结果了.
详解:
如图,过点D作DE⊥AB于点E,由题意可得∠ACB=75°,∠ABC=90°,DE=BC=42m,CD=BE,∠ADE=60°,
∴在Rt△ABC和Rt△ADE
AB=BCtan75°=42tan75°=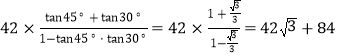 ,
,
AE=![]() ,
,
∴CD=AB﹣AE=![]() (米).
(米).
答:建筑物CD的高为84米.
睛:读懂题意,把已知量和未知量转化到Rt△ABC和Rt△ADE中,这样利用直角三角形中边角间的关系结合题目中所给的“两角和的三角形函数公式”即可使问题得到解决.

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案【题目】某出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人,行驶路程记录如下(规定向南为正,向北为负,单位:![]() ):
):
第1批 | 第2批 | 第3批 | 第4批 | 第5批 |
|
|
|
|
|
(1)接送完第5批客人时,该驾驶员在公司什么方向,距离公司多远?
(2)若该出租车的收费标准为:行驶路程不超过![]() ,收费10元;超过
,收费10元;超过![]() ,对超过部分另加收每千米1.8元.当送完第5批客人时,该驾驶员共收到车费多少元?
,对超过部分另加收每千米1.8元.当送完第5批客人时,该驾驶员共收到车费多少元?