题目内容
【题目】定义：若a+b＝2，则称a与b是关于1的平衡数．
（1）①3与 是关于1的平衡数；②4﹣x与 是关于1的平衡数（用含x的代数式表示）．
（2）若a＝2x2﹣3（x2+x）﹣4，b＝2x﹣[3x﹣（4x+x2）﹣2]，判断a与b是否是关于1的平衡数，并说明理由．
【答案】（1）①-1，②x﹣2；（2）不是，见解析
【解析】
（1）①根据平衡数的定义，可得3与﹣1是关于1的平衡数，
②4﹣x与x﹣2是关于1的平衡数；
（2）将两式相减得出a+b≠2，根据平衡数的定义，即可进行判断.
解：（1）①∵2-3=（﹣1），
∴3与﹣1是关于1的平衡数；
②∵
∴4﹣x与x﹣2是关于1的平衡数．
故答案为：﹣1；x﹣2；
（2）a＝2x2﹣3（x2+x）﹣4＝﹣x2﹣3x﹣4，
b＝2x﹣[3x﹣（4x+x2）﹣2]＝x2+3x+2，
a+b＝（﹣x2﹣3x﹣4）+（x2+3x+2）＝﹣2≠2．
因此，a与b不是关于1的平衡数．
【题目】某校为了做好大课间活动，计划用400元购买10件体育用品，备选体育用品及单价如下表（单位：元）
备选体育用品 | 篮球 | 排球 | 羽毛球拍 |
单价（元） | 50 | 40 | 25 |
（1）若400元全部用来购买篮球和羽毛球拍共10件，问篮球和羽毛球拍各购买多少件？
（2）若400元全部用来购买篮球、排球和羽毛球拍三种共10件，能实现吗？（若能实现直接写出一种答案即可，若不能请说明理由.）
【题目】甲、乙两校的学生人数基本相同，为了解这两所学校学生的数学学业水平，在某次测试中，从两校各随机抽取了30名学生的测试成绩进行调查分析，其中甲校已经绘制好了条形统计图，乙校只完成了一部分.
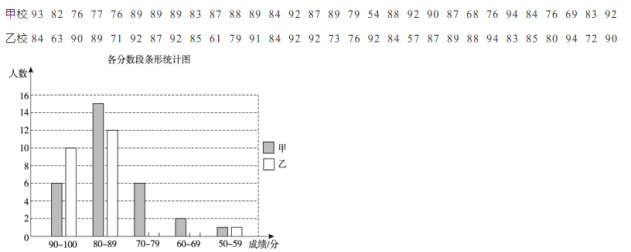
（1）请根据乙校的数据补全条形统计图：
（2）两组样本数据的平均数.中位数众数如下表所示，写出
、
的值：
平均数 | 中位数 | 众数 | |
甲校 |
|
|
|
乙校 |
|
|
|
（3）两所学校的同学都想依据抽样的数据说明自己学校学生的数学学业水平更好些，请为他们各写出条可以使用的理由；甲校：____.乙校：________.
（4）综合来看，可以推断出________校学生的数学学业水平更好些，理由为________.
