题目内容
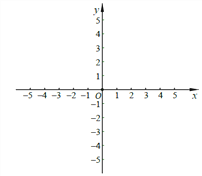
【题目】已知平而直角坐标系xOy(如图),二次函数y=ax2+bx+4的图像经过A(-2,0)、
B(4,0)两点,与y轴交于点C点.
(1)求这个二次函数的解析式;
(2)如果点E在线段OC上,且∠CBE=∠ACO,求点E的坐标;
(3)点M在y轴上,且位于点C上方,点N在直线BC上,点P为上述二次函数图像的对称轴上的点,如果以C、M、N、P为顶点的四边形是菱形,求点M的坐标.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() 或 M(0,6)
或 M(0,6)
【解析】分析:![]() 用待定系数法求二次函数解析式即可.
用待定系数法求二次函数解析式即可.
![]() 过点
过点![]() 作
作![]() 于点
于点![]() 在Rt△COB中,得出CH=EH.
在Rt△COB中,得出CH=EH.
在Rt△EBH中,![]() . 设
. 设![]() 则
则![]() CH=k,
CH=k,![]() .
.
列方程求解即可.
![]() 分3种情况进行讨论①当
分3种情况进行讨论①当![]() 为菱形
为菱形![]() 的边时,②当
的边时,②当![]() 为菱形
为菱形![]() 的边时,
的边时,
③当![]() 为菱形
为菱形![]() 的对角线时,分别求解即可.
的对角线时,分别求解即可.
详解:(1)∵ 抛物线![]() 与
与![]() 轴交于点A(-2,0),B(4,0),
轴交于点A(-2,0),B(4,0),
∴ ![]()
解得 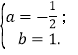
∴ 抛物线的解析式为![]()
(2)过点![]() 作
作![]() 于点
于点![]()
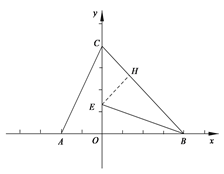
在Rt△ACO中, ∵A(-2,0),∴ OA=2,
当![]() 时
时 ![]() ∴OC=4,
∴OC=4,
在Rt△COB中,∵∠COB=90°,OC=OB=4,
∴![]() .
.
∵![]() ,∴CH=EH.
,∴CH=EH.
∴在Rt△ACO中,![]() ,
,
∵∠CBE=∠ACO,∴在Rt△EBH中,![]() .
.
设![]() 则
则![]() CH=k,
CH=k,![]() .
.
∴![]() .
.
∴![]()
∴![]()
∴![]() ∴
∴![]()
(3)∵ ![]()
∴抛物线的对称轴为直线![]()
①当![]() 为菱形
为菱形![]() 的边时,
的边时,
∴![]()
![]()
∵点P在二次函数的对称轴上,
点![]() 的横坐标为1,点
的横坐标为1,点![]() 的横坐标为1,
的横坐标为1,
∴![]() .
.
∵四边形![]() 是菱形,∴
是菱形,∴![]()
∴![]()
∴![]() .
.
②当![]() 为菱形
为菱形![]() 的边时,不存在,
的边时,不存在,
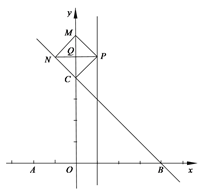
③当![]() 为菱形
为菱形![]() 的对角线时,
的对角线时,
设![]() 交
交![]() 于点
于点![]()
∴![]() 互相垂直平分,
互相垂直平分,
∴![]() .
.![]()
∵点![]() 在直线
在直线![]() 上,
上,![]()
在![]() 中,
中,![]()
∴![]() ∴
∴![]()
∴![]() ∴
∴![]()
∴ ![]()
∴综上所述![]() 或 M(0,6).
或 M(0,6).

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目