题目内容
如图, 在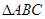 中,
中, 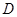 是
是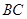 边上的一点,
边上的一点, 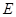 是
是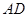 的中点, 过
的中点, 过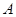 点作
点作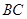 的平行线交
的平行线交 的延长线于点
的延长线于点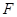 , 且
, 且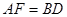 , 连接
, 连接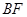 .
.
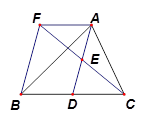
(1) 求证: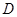 是
是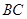 的中点;
的中点;
(2) 若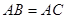 , 试判断四边形
, 试判断四边形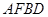 的形状, 并证明你的结论.
的形状, 并证明你的结论.
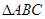 中,
中, 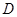 是
是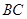 边上的一点,
边上的一点, 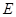 是
是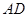 的中点, 过
的中点, 过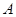 点作
点作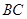 的平行线交
的平行线交 的延长线于点
的延长线于点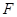 , 且
, 且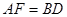 , 连接
, 连接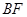 .
.
(1) 求证:
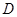 是
是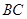 的中点;
的中点;(2) 若
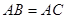 , 试判断四边形
, 试判断四边形 的形状, 并证明你的结论.
的形状, 并证明你的结论. (1)通过证明BD=CD,得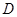 是
是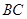 的中点 (2)AFBD是矩形
的中点 (2)AFBD是矩形
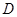 是
是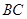 的中点 (2)AFBD是矩形
的中点 (2)AFBD是矩形试题分析:(1)在
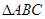 中,
中, 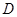 是
是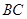 边上的一点,
边上的一点, 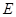 是
是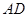 的中点,则AE=DE;过
的中点,则AE=DE;过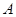 点作
点作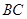 的平行线交
的平行线交 的延长线于点
的延长线于点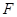 , 即AF//CD,得
, 即AF//CD,得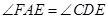 ;又因为
;又因为 (对顶角相等),所以
(对顶角相等),所以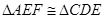 ,所以AF=CD;
,所以AF=CD;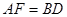 ,所以BD=CD,所以D是BC的中点
,所以BD=CD,所以D是BC的中点(2)过
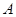 点作
点作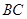 的平行线交
的平行线交 的延长线于点
的延长线于点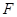 , 且
, 且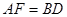 , 连接
, 连接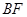 .
.∵AF//BD,AF=BD
∴四边形AFBD是平行四边形,AD=BF,
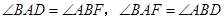
在
 中由(1)的证明知
中由(1)的证明知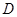 是
是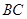 的中点,AF=CD
的中点,AF=CD∵
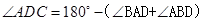 ,
,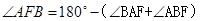
∴
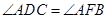
∴
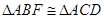
所以AB=AC;D是BC的中点
所以AD⊥BC,
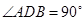
∴平行四边形AFBD是矩形
点评:本题考查三角形全等和矩形,解本题的关键是掌握判定三角形全等的方法,会判定一个四边形是否是矩形

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 、
、 是方格纸的两个格点(即正方形的顶点),在这个
是方格纸的两个格点(即正方形的顶点),在这个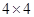 的方格纸中,找出格点
的方格纸中,找出格点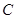 ,使
,使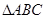 是等腰三角形,这样的点
是等腰三角形,这样的点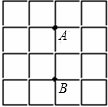
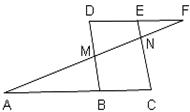
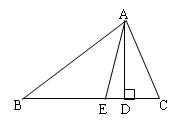
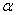 (∠C>∠B),求∠DAE的度数(用含
(∠C>∠B),求∠DAE的度数(用含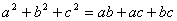 ,则△ABC是 三角形。
,则△ABC是 三角形。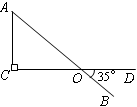
 。其中能构成直角三角形的有( )组
。其中能构成直角三角形的有( )组 