Question

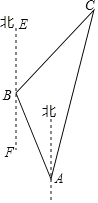
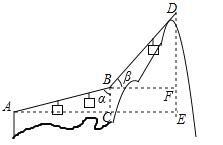
【题目】（2017安徽省）如图，游客在点A处做缆车出发，沿A﹣B﹣D的路线可至山顶D处，假设AB和BD都是直线段，且AB=BD=600m，α=75°，β=45°，求DE的长．

（参考数据：sin75°≈0.97，cos75°≈0.26，≈1.41）

Answer 1

【答案】579m．

【解析】试题分析：分别在Rt△ABC中和Rt△BDF中利用三角函数求得BC和DF长，再根据EF=BC，便可求得DE=DF+EF.

解：在Rt△ABC中，∵AB＝600m，∠ABC＝75°，∴BC＝AB·cos75°≈600×0.26＝156(m)．

在Rt△BDF中，∵BD=600m，∠DBF＝45°，∴DF＝BD·sin45°＝600×≈300×1.41＝423(m)．

∵四边形BCEF是矩形，∴EF＝BC＝156(m)，

∴DE＝DF＋EF＝423＋156＝579(m)．

答：DE的长为579m.