题目内容
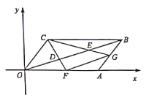
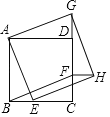
【题目】如图，四边形 ABCD 是正方形，点 E，F 分别在 BC，CD 上，点 G 在 CD 的延长线上，且 BE=CF=DG 以线段AE，AG 为两邻边作 AEHG．
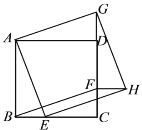
（1）求证：四边形 BEHF 是平行四边形．
（2）若四边形 ABCD 与 AEHG 的面积分别为 16，18．试求四边形 BEHF 的面积．
【答案】（1）证明见解析；（2）2．
【解析】
（1）由△ABE≌△BCF≌△ADG，推出AE=BF=AG，∠BAE=∠DAG，推出∠EAG=∠BAD=90°，由四边形AEHG是平行四边形，AG=AE，∠EAG=90°，推出四边形AEHG是正方形，再证明BF=EH，BF∥EH即可解决问题；
（2）根据S平行四边形BEHF=BECF，只要求出BE、CF即可解决问题．
（1）∵四边形BCD是正方形，∴AB=BC=CD=AD，∠ABE=∠BCF=∠ADG=90°．
∵BE=CF=DG，∴△ABE≌△BCF≌△ADG，∴AE=BF=AG，∠BAE=∠DAG，∴∠EAG=∠BAD=90°．
∵四边形AEHG是平行四边形，AG=AE，∠EAG=90°，∴四边形AEHG是正方形．
∵∠BAE=∠CBF，∠CBF+∠ABF=90°，∴∠BAE+∠ABF=90°，∴AE⊥BF．
∵EH⊥AE，∴BF∥EH．
∵BF=AG=EH，∴四边形BEHF是平行四边形．
（2）∵四边形ABCD与AEHG的面积分别为16，18，四边形ABCD与AEHG都是正方形，∴AB=4，AE=3
．在Rt△ABE中，BE
，∴CF=BE
，∴S平行四边形BEHF=BECF=2．
练习册系列答案
名校课堂系列答案
相关题目
