题目内容
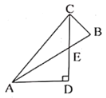
【题目】如图,在等腰△ABC中,AB=AC,∠A=20°.AB上一点D,使AD=BC,过点D作DE∥BC且DE=AB,连接EC,则∠DCE=_____°.
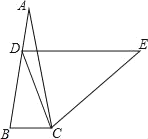
【答案】70
【解析】
连接AE.根据SAS可证△ADE≌△CBA,可得AE=AC,∠AED=∠BAC=20°,根据等边三角形的判定可得△ACE是等边三角形,根据等腰三角形的判定可得△DCE是等腰三角形,再根据三角形内角和定理和角的和差关系即可求解.
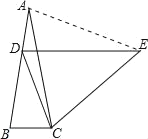
解:如图所示,连接AE.
∵DE∥BC,
∴∠ADE=∠B,
在△ADE与△CBA中, 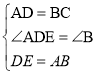
∴△ADE≌△CBA(SAS),
∵AB=AC,∠BAC=20°,
∴AE=AC=AB=DE,∠AED=∠BAC=20°,∠DAE=∠ADE=∠B=∠ACB=80°,
∵∠CAE=∠DAE﹣∠BAC=80°﹣20°=60°,
∴△ACE是等边三角形,
∴CE=AC=AE=DE,∠AEC=∠ACE=60°,
∴△DCE是等腰三角形,
∴∠CDE=∠DCE,
∴∠DEC=∠AEC﹣∠AED=40°,
∴∠DCE=∠CDE=(180﹣40°)÷2=70°.
故答案为:70.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目