题目内容

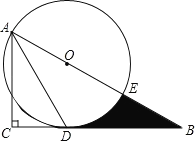
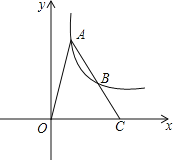
【题目】如图，平行四边形ABCD中，E为AD的中点，已知△DEF的面积为S，则四边形ABCE的面积为（　　）

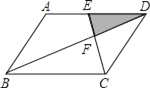
A. 8S B. 9S C. 10S D. 11S

【答案】B

【解析】分析：由于四边形ABCD是平行四边形，那么AD∥BC，AD=BC，根据平行线分线段成比例定理的推论可得△DEF∽△BCF，再根据E是AD中点，易求出相似比，从而可求的面积，再利用与是同高的三角形，则两个三角形面积比等于它们的底之比，从而易求的面积，进而可求的面积．

详解：如图所示，

∵四边形ABCD是平行四边形，

∴AD∥BC，AD=BC，

∴△DEF∽△BCF，

∴

又∵E是AD中点，

∴

∴DE:BC=DF:BF=1:2，

∴

∴

又∵DF:BF=1:2，

∴

∴

∴四边形ABCE的面积=9S，

故选B.

练习册系列答案
相关题目

【题目】如图，在Rt△ABC中，∠C=90°，∠BAC的角平分线AD交BC边于D．以AB上某一点O为圆心作⊙O，使⊙O经过点A和点D．

（1）判断直线BC与⊙O的位置关系，并说明理由；

（2）若AC=3，∠B=30°．

①求⊙O的半径；

②设⊙O与AB边的另一个交点为E，求线段BD、BE与劣弧DE所围成的阴影部分的图形面积．（结果保留根号和π）

【题目】某市去年成功举办2018郴州国际休闲旅游文化节，获评“全国森林旅游示范市”．某市有A，B，C，D，E五个景区很受游客喜爱．一旅行社对某小区居民在暑假期间去以上五个景区旅游（只选一个景区）的意向做了一次随机调查统计，并根据这个统计结果制作了如下两幅不完整的统计图：

（1）该小区居民在这次随机调查中被调查到的人数是　 　人，　 　，并补全条形统计图；

（2）若该小区有居民1200人，试估计去B地旅游的居民约有多少人？

（3）小军同学已去过E地旅游，暑假期间计划与父母从A，B，C，D四个景区中，任选两个去旅游，求选到A，C两个景区的概率．（要求画树状图或列表求概率）

【题目】如图，要设计一副宽20 cm、长30 cm的图案，其中有一横一竖的彩条，横、竖彩条的宽度之比为2∶3．如果要彩条所占面积是图案面积的19%，问横、竖彩条的宽度各为多少cm？

【题目】在平面直角坐标系中，抛物线经过点，、，，其中、是方程的两根，且，过点的直线与抛物线只有一个公共点

（1）求、两点的坐标；

（2）求直线的解析式；

（3）如图2，点是线段上的动点，若过点作轴的平行线与直线相交于点，与抛物线相交于点，过点作的平行线与直线相交于点，求的长．

【题目】如图所示，矩形中，厘米，厘米（）．动点同时从点出发，分别沿，运动，速度是厘米／秒．过作直线垂直于，分别交，于．当点到达终点时，点也随之停止运动．设运动时间为秒．

（1）若厘米，秒，求PM的长度；

（2）若厘米，求出某个时间，使⊿PNB∽⊿PAD，并求出它们的相似比；

（3）若在运动过程中，存在某时刻使梯形PMBN与梯形PQDA的面积相等，求的取值范围；

【题目】如图，AB为⊙O直径，C是⊙O上一点，CO⊥AB于点O，弦CD与AB交于点F，在AB的延长线上取一点E，使EF＝ED，过点A作⊙O的切线交ED的延长线于点G.

（1）求证：GE是⊙O的切线；

（2）若OF：OB＝1：3，⊙O的半径为3，求DE和AG的长．

【题目】如图，A、B是双曲线上的点，点A的坐标是是线段AC的中点．

求k的值；

求点B的坐标；

求的面积．

【题目】如图，菱形ABCD中，对角线AC＝6，BD＝8，M、N分别是BC、CD上的动点，P是线段BD上的一个动点，则PM＋PN的最小值是（ ）

A. B. C. D.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网