Question

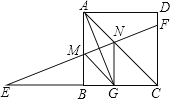
【题目】如图，在正方形ABCD中，∠BAC的平分线交BC边于G，AG的中垂线与CB的延长线交于E，与AB、AC、DC分别交于点M，N，F，下列结论：①tan∠E=，②△AGC≌△EMG，③四边形AMGN是菱形，④S△CFN=S四边形AMGN，其中正确的是______（填序号）．

Answer 1

【答案】②③④

【解析】

在正方形ABCD中，∠BAC的平分线交BC边于G，可得∠BAG=∠CAG=∠BAC=22.5°，∠AGB=67.5°，因为AG的中垂线与CB的延长线交于E，可得AM=MG，AN=NG，∠E=22.5°，即可判断①错误，证明AM=AN，可得AM=GM=NG=AN，即四边形AMGN是菱形，可判断③正确；用“角角边”可证明△AGC≌△EMG，可判断②正确；证明意△AMN∽△CFN，可得S△CFN=2S△AMN=S四边形AMGN，可判断④正确．

解：∵在正方形ABCD中，∠BAC的平分线交BC边于G，

∴∠BAG=∠CAG=∠BAC=22.5°，

∵∠ABC=90°，

∴∠AGB=90°-22.5°=67.5°，

∵AG的中垂线与CB的延长线交于E，

∴AM=MG，AN=NG，∠E=90°-∠AGB=22.5°，

∴tan∠E=错误，即①错误；

∵∠AMN=∠ANM=90°-22.5°=67.5°，

∴AM=AN，

∴AM=GM=NG=AN，

∴四边形AMGN是菱形，即③正确；

∵四边形AMGN是菱形，

∴MG∥AC，AB∥NG，

∴∠ACG=∠MGE=45°，∠NGC=∠ABC=90°，

∴GC=GN=GM，

∵∠GAC=∠E=22.5°，

∴△AGC≌△EMG（AAS），即②正确；

由题意△AMN∽△CFN，

∴，

∴S△CFN=2S△AMN=S四边形AMGN，即④正确．

故答案为：②③④．