Question

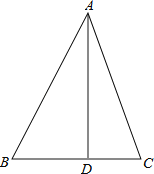
【题目】如图，在△ABC中，∠BAC＝45°，AD⊥BC于点D，若BD＝3，CD＝2．则△ABC的面积为_____．

Answer 1

【答案】15

【解析】

将△ABD绕着点A逆时针旋转90°，得△AFQ，延长FQ，BC，交于点E，连接CQ，判定△BAC≌△QAC（SAS），得到BC=CQ=BD+CD=5，再设AD=x，在Rt△CQE中，运用勾股定理列出关于x的方程，求得x的值，最后根据△ABC的面积=×BC×AD，进行计算即可

解：如图，将△ABD绕着点A逆时针旋转90°，得△AFQ，延长FQ，BC，交于点E，连接CQ，

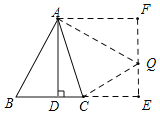
由旋转可得，△ABD≌△AQF，

∴AB＝AQ，∠BAD＝∠FAQ，BD＝QF＝3，∠F＝∠ADC＝∠DAF＝90°＝∠E，

∵∠BAC＝45°，

∴∠BAD+∠DAC＝45°，

∴∠DAC+∠FAQ＝45°，

又∵∠DAF＝90°，

∴∠CAQ＝45°，

∴∠BAC＝∠CAQ．且AB＝AQ，AC＝AC

∴△BAC≌△QAC（SAS），

∴BC＝CQ＝BD+CD＝5，

设AD＝x，则QE＝x﹣3，CE＝x﹣2．

在Rt△CQE中，CE2+QE2＝CQ2

∴（x﹣2）2+（x﹣3）2＝52

解得：x1＝6，x2＝﹣1（舍去），

∴AD＝6，

∴△ABC的面积为＝×BC×AD＝15

故答案为：15