题目内容
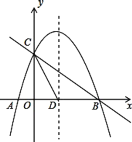
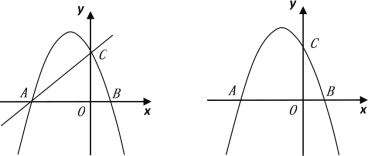
【题目】如图,抛物线y=﹣x2﹣2x+3 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C.
(1)求A、B、C的坐标;
(2)过抛物线上一点F作y轴的平行线,与直线AC交于点G.若FG=![]() AC,求点F的坐标;
AC,求点F的坐标;
(3)E(0,﹣2),连接BE.将△OBE绕平面内的某点逆时针旋转90°得到△O′B′E′,O、B、E的对应点分别为O′、B′、E′.若点B′、E′两点恰好落在抛物线上,求点B′的坐标.
【答案】(1)A(﹣3,0);B(1,0);C(0,3);(2)F点的坐标为(﹣1,4)或(﹣2,3)或(![]() ,
,![]()
![]() )或(
)或(![]() ,
,![]() );(3)(
);(3)(![]() ,
,![]() ).
).
【解析】
(1)对于抛物线分别令x=0,y=0即可求解;
(2)先求出AC的解析式,由题意可知FG=2,设F(m,-m2-2m+3),则G(m,m+3),则有|-m2-2m+3-(m+3)|=2,解方程即可;
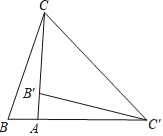
(3)如图2中,旋转90°后,对应线段互相垂直且相等,则BE与![]() 互相垂直且相等.设
互相垂直且相等.设![]() (t,-t2-2t+3),则
(t,-t2-2t+3),则![]() (t+2,-t2-2t+3-1).因为
(t+2,-t2-2t+3-1).因为![]() 在抛物线上,则有-(t+2)2-2(t+2)+3=-t2-2t+3-1,解方程即可.
在抛物线上,则有-(t+2)2-2(t+2)+3=-t2-2t+3-1,解方程即可.
(1)对于抛物线y=﹣x2﹣2x+3,
令x=0得y=3,
∴C(0,3),
令y=0,则﹣x2﹣2x+3=0解得x=﹣3或1,
∴A(﹣3,0),B(1,0);C(0,3).
(2)如图1中,
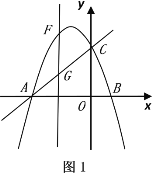
∵A(﹣3,0),C(0,3),
∴直线AC解析式为y=x+3,OA=OC=3,
∴AC=3![]() ,FG=
,FG=![]() AC=2,
AC=2,
设F(m,﹣m2﹣2m+3),则G(m,m+3),
则|﹣m2﹣2m+3﹣(m+3)|=2,
解得m=﹣1或﹣2或![]() 或
或![]() ,
,
则F点的坐标为(﹣1,4)或(﹣2,3)或(![]() ,
,![]()
![]() )或(
)或(![]() ,
,![]() ).
).
(3)如图2中,旋转90°后,对应线段互相垂直且相等,则BE与B’E’互相垂直且相等.
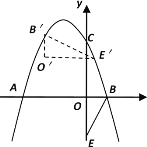
设B′(t,﹣t2﹣2t+3),则E′(t+2,﹣t2﹣2t+3﹣1),
∵E′在抛物线上,则﹣(t+2)2﹣2(t+2)+3=﹣t2﹣2t+3﹣1,
解得:t=![]() ,则B′的坐标为(
,则B′的坐标为(![]() ,
,![]() ).
).

 名校课堂系列答案
名校课堂系列答案