题目内容
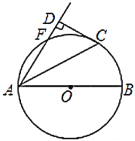
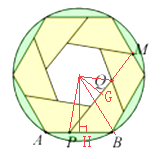
【题目】小明发现相机快门打开过程中,光圈大小变化如图1所示,于是他绘制了如图2所示的图形.图2中留个形状大小都相同的四边形围成一个圆的内接六边形和一个小正六边形,若PQ所在的直线经过点M,PB=5cm,小正六边形的面积为![]() cm2,则该圆的半径为________cm.
cm2,则该圆的半径为________cm.

【答案】8.
【解析】分析: 设两个正六边形的中心为O,连接OP,OB,过点O作OG⊥PM于点G,OH⊥AB于点H,如图所示:很容易证出三角形PMN是一个等边三角形,边长PM的长,,而且面积等于小正六边形的面积的![]() , 故三角形PMN的面积很容易被求出,根据正六边形的性质及等腰三角形的三线和一可以得出PG的长,进而得出OG的长,,在Rt△OPG中,根据勾股定理得 OP的长,设OB为x,,根据正六边形的性质及等腰三角形的三线和一可以得出BH,OH的长,进而得出PH的长,在Rt△PHO中,根据勾股定理得关于x的方程,求解得出x的值,从而得出答案.
, 故三角形PMN的面积很容易被求出,根据正六边形的性质及等腰三角形的三线和一可以得出PG的长,进而得出OG的长,,在Rt△OPG中,根据勾股定理得 OP的长,设OB为x,,根据正六边形的性质及等腰三角形的三线和一可以得出BH,OH的长,进而得出PH的长,在Rt△PHO中,根据勾股定理得关于x的方程,求解得出x的值,从而得出答案.
详解: 设两个正六边形的中心为O,连接OP,OB,过点O作OG⊥PM于点G,OH⊥AB于点H,如图所示:
很容易证出三角形PMN是一个等边三角形,边长PM=![]() ,而且面积等于小正六边形的面积的
,而且面积等于小正六边形的面积的![]() ,
,
故三角形PMN的面积为![]() cm2,
cm2,
∵OG⊥PM,且O是正六边形的中心,
∴PG=![]() PM=
PM=![]()
∴OG=![]() ,
,
在Rt△OPG中,根据勾股定理得 :OP2=OG2+PG2,即![]() =OP2,
=OP2,
∴OP=7cm,
设OB为x,
∵OH⊥AB,且O是正六边形的中心,
∴BH=![]() X,OH=
X,OH=![]() ,
,
∴PH=5-![]() x,
x,
在Rt△PHO中,根据勾股定理得OP2=PH2+OH2,即![]() ;
;
解得:x1=8,x2=-3(舍)
故该圆的半径为8cm.
故答案为:8.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目