Ő‚ńŅńŕ»›
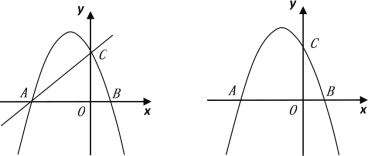
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ň◊őÔŌŖy= ![]() x2+mx+n”Žx÷ŠĹĽ”ŕA°ĘBŃĹĶ„£¨”Žy÷ŠĹĽ”ŕĶ„C£¨Ň◊őÔŌŖĶń∂‘≥∆÷ŠĹĽx÷Š”ŕĶ„D£¨“—÷™A(1£¨0)£¨C(0£¨2)£ģ
x2+mx+n”Žx÷ŠĹĽ”ŕA°ĘBŃĹĶ„£¨”Žy÷ŠĹĽ”ŕĶ„C£¨Ň◊őÔŌŖĶń∂‘≥∆÷ŠĹĽx÷Š”ŕĶ„D£¨“—÷™A(1£¨0)£¨C(0£¨2)£ģ
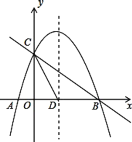
(1)«ůŇ◊őÔŌŖĶńĪŪīÔ Ĺ£Ľ
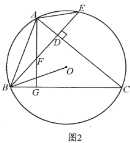
(2) «Žń„‘ŕŇ◊őÔŌŖĶń∂‘≥∆÷Š…Ō’“Ķ„P£¨ Ļ°ųPCD «“‘CDő™—ŁĶńĶ»—Ł»żĹ«–ő£¨ňý”–∑ŻļŌŐűľĢĶńĶ„PĶń◊ÝĪÍ∑÷Īūő™ £Ľ
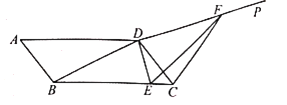
(3)Ķ„E «ŌŖ∂őBC…ŌĶń“ĽłŲ∂ĮĶ„£¨ĻżĶ„E◊ųx÷ŠĶńīĻŌŖ”ŽŇ◊őÔŌŖŌŗĹĽ”ŕĶ„F£¨ĶĪĶ„E‘ň∂ĮĶĹ ≤√īőĽ÷√ Ī£¨ňńĪŖ–őCDBFĶń√śĽż◊Óīů?«ů≥ŲňńĪŖ–őCDBFĶń◊Óīů√śĽżľįīň ĪEĶ„Ķń◊ÝĪÍ£ģ
°ĺīūįł°Ņ£®1£©y=©Ā![]() x2+
x2+![]() x+2£Ľ£®2£©P1£®
x+2£Ľ£®2£©P1£®![]() £¨4£©£¨P2£®
£¨4£©£¨P2£®![]() £¨
£¨![]() £©£¨P3£®
£©£¨P3£®![]() £¨©Ā
£¨©Ā![]() £©£Ľ£®3£©SňńĪŖ–őCDBFĶń√śĽż◊Óīů=
£©£Ľ£®3£©SňńĪŖ–őCDBFĶń√śĽż◊Óīů=![]() £¨E£®2£¨1£©
£¨E£®2£¨1£©
°ĺĹ‚őŲ°Ņ
£®1£©÷ĪĹ”į—AĶ„ļÕCĶ„◊ÝĪÍīķ»Žy=©Ā![]() x2+mx+nĶ√m°ĘnĶń∑Ĺ≥Ő◊ť£¨»ĽļůĹ‚∑Ĺ≥Ő◊ť«ů≥Ųm°ĘnľīŅ…Ķ√ĶĹŇ◊őÔŌŖĹ‚őŲ Ĺ£Ľ
x2+mx+nĶ√m°ĘnĶń∑Ĺ≥Ő◊ť£¨»ĽļůĹ‚∑Ĺ≥Ő◊ť«ů≥Ųm°ĘnľīŅ…Ķ√ĶĹŇ◊őÔŌŖĹ‚őŲ Ĺ£Ľ
£®2£©Ō»ņŻ”√Ň◊őÔŌŖ∂‘≥∆÷Š∑Ĺ≥Ő«ů≥ŲŇ◊őÔŌŖĶń∂‘≥∆÷Šő™÷ĪŌŖx=©Ā![]() £¨‘ÚD£®
£¨‘ÚD£®![]() £¨0£©£¨‘ÚņŻ”√ĻīĻ…∂®ņŪľ∆ň„≥ŲCD=
£¨0£©£¨‘ÚņŻ”√ĻīĻ…∂®ņŪľ∆ň„≥ŲCD=![]() £¨»Ľļů∑÷ņŗŐ÷¬Ř£ļ»ÁÕľ1£¨ĶĪCP=CD Ī£¨ņŻ”√Ķ»—Ł»żĹ«–őĶń–‘÷ “◊Ķ√P1£®
£¨»Ľļů∑÷ņŗŐ÷¬Ř£ļ»ÁÕľ1£¨ĶĪCP=CD Ī£¨ņŻ”√Ķ»—Ł»żĹ«–őĶń–‘÷ “◊Ķ√P1£®![]() £¨4£©£ĽĶĪDP=DC Ī£¨“◊Ķ√P2£®
£¨4£©£ĽĶĪDP=DC Ī£¨“◊Ķ√P2£®![]() £¨
£¨![]() £©£¨P3£®
£©£¨P3£®![]() £¨©Ā
£¨©Ā![]() £©£Ľ
£©£Ľ
£®3£©Ō»łýĺ›Ň◊őÔŌŖ”Žx÷ŠĶńĹĽĶ„ő Ő‚«ů≥ŲB£®4£¨0£©£¨‘ŔņŻ”√īż∂®ŌĶ ż∑®«ů≥Ų÷ĪŌŖBCĶńĹ‚őŲ Ĺő™y=©Ā![]() x+2£¨ņŻ”√“ĽīőļĮ żÕľŌů…ŌĶ„Ķń◊ÝĪÍŐō’ųļÕ∂ĢīőļĮ żÕľŌů…ŌĶ„Ķń◊ÝĪÍŐō’ų£¨…ŤE£®x£¨©Ā
x+2£¨ņŻ”√“ĽīőļĮ żÕľŌů…ŌĶ„Ķń◊ÝĪÍŐō’ųļÕ∂ĢīőļĮ żÕľŌů…ŌĶ„Ķń◊ÝĪÍŐō’ų£¨…ŤE£®x£¨©Ā![]() x+2£©£®0°‹x°‹4£©£¨‘ÚF£®x£¨©Ā
x+2£©£®0°‹x°‹4£©£¨‘ÚF£®x£¨©Ā![]() x2+
x2+![]() x+2£©£¨‘ÚFE=©Ā
x+2£©£¨‘ÚFE=©Ā![]() x2+2x£¨”…”ŕ°ųBEFļÕ°ųCEFĻ≤Ķ◊ĪŖ£¨łŖĶńļÕő™4£¨‘ÚS°ųBCF=S°ųBEF+S°ųCEF=
x2+2x£¨”…”ŕ°ųBEFļÕ°ųCEFĻ≤Ķ◊ĪŖ£¨łŖĶńļÕő™4£¨‘ÚS°ųBCF=S°ųBEF+S°ųCEF=![]() 4EF=©Āx2+4x£¨ľ”…ŌS°ųBCD=
4EF=©Āx2+4x£¨ľ”…ŌS°ųBCD=![]() £¨ňý“‘SňńĪŖ–őCDBF=S°ųBCF+S°ųBCD=©Āx2+4x+
£¨ňý“‘SňńĪŖ–őCDBF=S°ųBCF+S°ųBCD=©Āx2+4x+![]() £®0°‹x°‹4£©£¨»Ľļůłýĺ›∂ĢīőļĮ żĶń–‘÷ «ůňńĪŖ–őCDBFĶń√śĽż◊Óīů£¨≤ĘĶ√ĶĹīň ĪEĶ„◊ÝĪÍ£ģ
£®0°‹x°‹4£©£¨»Ľļůłýĺ›∂ĢīőļĮ żĶń–‘÷ «ůňńĪŖ–őCDBFĶń√śĽż◊Óīů£¨≤ĘĶ√ĶĹīň ĪEĶ„◊ÝĪÍ£ģ
£®1£©°ŖŇ◊őÔŌŖy=©Ā![]() x2+mx+nĺ≠ĻżA£®©Ā1£¨0£©£¨C£®0£¨2£©£ģ
x2+mx+nĺ≠ĻżA£®©Ā1£¨0£©£¨C£®0£¨2£©£ģ
°ŗ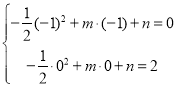 Ĺ‚Ķ√£ļ
Ĺ‚Ķ√£ļ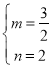 £¨
£¨
°ŗŇ◊őÔŌŖĶńĹ‚őŲ Ĺő™£ļy=©Ā![]() x2+
x2+![]() x+2£Ľ
x+2£Ľ
£®2£©Ň◊őÔŌŖĶń∂‘≥∆÷Šő™÷ĪŌŖ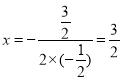 £¨‘ÚD£®
£¨‘ÚD£®![]() £¨0£©£¨
£¨0£©£¨
°ŗ![]() £¨
£¨
»ÁÕľ1£¨
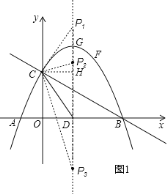
ĶĪCP=CD Ī£¨‘ÚP1£®![]() £¨4£©£Ľ
£¨4£©£Ľ
ĶĪDP=DC Ī£¨‘ÚP2£®![]() £¨
£¨![]() £©£¨P3£®
£©£¨P3£®![]() £¨©Ā
£¨©Ā![]() £©£¨
£©£¨
◊Ř…Ōňý Ų£¨¬ķ◊„ŐűľĢĶńPĶ„◊ÝĪÍő™P1£®![]() £¨4£©£¨P2£®
£¨4£©£¨P2£®![]() £¨
£¨![]() £©£¨P3£®
£©£¨P3£®![]() £¨©Ā
£¨©Ā![]() £©£Ľ
£©£Ľ
£®3£©ĶĪy=0 Ī£¨0=©Ā![]() x2+
x2+![]() x+2
x+2
°ŗx1=©Ā1£¨x2=4£¨°ŗB£®4£¨0£©£ģ
…Ť÷ĪŌŖBCĶńĹ‚őŲ Ĺő™y=kx+b£¨”…ÕľŌů£¨Ķ√
![]() £¨Ĺ‚Ķ√£ļ
£¨Ĺ‚Ķ√£ļ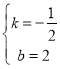 £¨
£¨
°ŗ÷ĪŌŖBCĶńĹ‚őŲ Ĺő™£ļy=©Ā![]() x+2£ģ
x+2£ģ
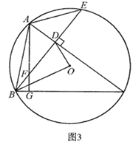
»ÁÕľ2£¨ĻżĶ„C◊ųCM°ÕEF”ŕM£¨
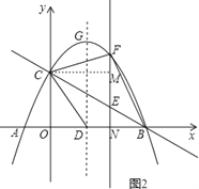
…ŤE£®a£¨©Ā![]() a+2£©£¨F£®a£¨©Ā
a+2£©£¨F£®a£¨©Ā![]() a2+
a2+![]() a+2£©£¨
a+2£©£¨
°ŗEF=©Ā![]() a2+
a2+![]() a+2©Ā£®©Ā
a+2©Ā£®©Ā![]() a+2£©=©Ā
a+2£©=©Ā![]() a2+2a£®0°‹x°‹4£©£ģ
a2+2a£®0°‹x°‹4£©£ģ
°ŖSňńĪŖ–őCDBF=S°ųBCD+S°ųCEF+S°ųBEF=![]() BDOC+
BDOC+![]() EFCM+
EFCM+![]() EFBN£¨
EFBN£¨
=![]() +
+![]() a£®©Ā
a£®©Ā![]() a2+2a£©+
a2+2a£©+![]() £®4©Āa£©£®©Ā
£®4©Āa£©£®©Ā![]() a2+2a£©£¨
a2+2a£©£¨
=©Āa2+4a+![]() £®0°‹x°‹4£©£ģ=©Ā£®a©Ā2£©2+
£®0°‹x°‹4£©£ģ=©Ā£®a©Ā2£©2+![]()
°ŗa=2 Ī£¨SňńĪŖ–őCDBFĶń√śĽż◊Óīů=![]() £¨
£¨
°ŗE£®2£¨1£©£ģ