Question

【题目】已知：△ABC与△ABD中，∠CAB＝∠DBA＝β，且∠ADB＋∠ACB＝180°．

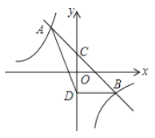
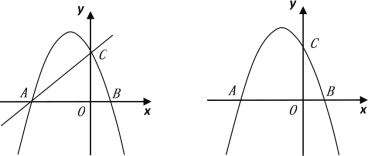
提出问题：如图1，当∠ADB＝∠ACB＝90°时，求证：AD＝BC；

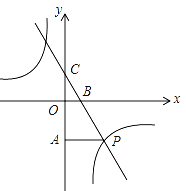
类比探究：如图2，当∠ADB≠∠ACB时，AD＝BC是否还成立？并说明理由．

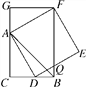
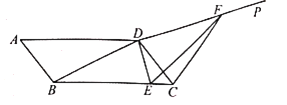
综合运用：如图3，当β＝18°，BC＝1，且AB⊥BC时，求AC的长．

Answer 1

【答案】（1）见解析；（2）仍然成立，理由见解析；（3）＋1

【解析】

（1）证明△DBA≌△CAB即可；

（2）作∠BEC＝∠BCE，BE交AC于E，证明△DBA≌△EAB即可；

（3）作∠BEC＝∠BCE，BE交AC于E，由（2）得，AD＝BC＝BE＝1，通过角之间的关系可求得EF＝BE＝1，再证△CBE∽△CFB，根据相似三角形的对应边成比例求解即可．

（1）在△BDA和△CAB中

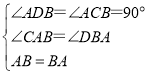
∴△DBA≌△CAB(AAS)；

（2）结论仍然成立．

理由：作∠BEC＝∠BCE，BE交AC于E．

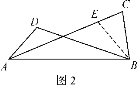
∵∠ADB＋∠ACB＝∠AEB＋∠BEC＝180°

∴∠ADB＝∠AEB．

又∠CAB＝∠DBA，AB=BA

∴△DBA≌△EAB(AAS)，

∴BE＝AD，

∵∠BEC＝∠BCE，

∴BC＝BE，

∴AD＝BC．

（3）作∠BEC＝∠BCE，BE交AC于E,

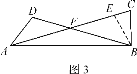
由（2）得，AD＝BC＝BE＝1

在Rt△ACB中，∠CAB＝18°

∴∠C＝72°，∠BEC＝∠C＝ 72°

由∠CFB＝∠CAB＋∠DBA＝36°

∴∠EBF＝∠CEB－∠CFB＝36°

∴EF＝BE＝1

在△BCF中，∠FBC＝180°－∠BFC－∠C＝72°

∴∠FBC＝∠BEC，∠C＝∠C

∴△CBE∽△CFB

∴＝

令CE＝x，∴1＝x(x＋1)

解之，x＝

∴CF＝

由∠FBC＝∠BEC

∴BF＝CF．又AF＝BF

∴AC＝2CF＝＋1