题目内容
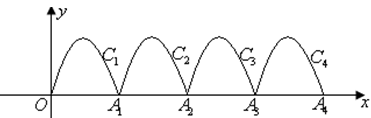
如图,抛物线y=-x2+2x+m(m<0)与x轴相交于点A(x1,0)、B(x2,0),点A在点B的左侧.当x=x2-2时,y______0(填“>”“=”或“<”号).
<.
解析试题分析:本题考查了二次函数根与系数的关系,由根与系数的关系得到m小于0,并能求出x=x2-2小于0,结合图象从而求得y值的大于0.
解:∵抛物线y=-x2+2x+m(m<0)与x轴相交于点A(x1,0)、B(x2,0),
∴x1+x2=2,x1x2=-m>0,
∴m<0,x1>0,x2>0,
∵x1+x2=2
∴x1=2-x2
∴x=-x1<0
∴y<0
故答案为<.
考点:抛物线与x轴的交点.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
抛物线 上部分点的横坐标
上部分点的横坐标 ,纵坐标
,纵坐标 的对应值如下表:
的对应值如下表:
 | … |  |  | 0 | 1 | 2 | … |
 | … | 0 | 4 | 6 | 6 | 4 | … |
①抛物线与
 轴的一个交点为
轴的一个交点为 ; ②抛物线与
; ②抛物线与 轴的交点为
轴的交点为 ;
;③抛物线的对称轴是:直线
 ; ④在对称轴左侧
; ④在对称轴左侧 随
随 增大而增大.
增大而增大.  的图象最高点的纵坐标为0,则m的值为
的图象最高点的纵坐标为0,则m的值为  关于底面的一条边长x
关于底面的一条边长x 的函数解析式是 .其中x的取值范围是 .
的函数解析式是 .其中x的取值范围是 .
 x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是 .
x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是 .
 的最小值是 .
的最小值是 .
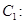
 与
与 轴交于点
轴交于点 ,
, ;将
;将 向右平移得第2段抛物线
向右平移得第2段抛物线 ,交
,交 ;再将
;再将 ,交
,交 ;又将
;又将 ,交
,交 ,若
,若 在
在 的值是 .
的值是 .