��Ŀ����
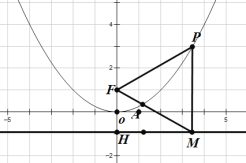
����Ŀ����ֱ֪��y=x+3��x���ڵ�A����y���ڵ�B��������y=![]() x2+bx+c������A��B��
x2+bx+c������A��B��
��1���������߽���ʽ��
��2����C��m��0�����߶�OA�ϣ���C����A��O���غϣ���CD��OA��AB�ڵ�D�����������ڵ�E����DE=![]() AD����m��ֵ��
AD����m��ֵ��
��3����M���������ϣ���N�������ߵĶԳ����ϣ��ڣ�2���������£��Ƿ�����Ե�D��B��M��NΪ������ı���Ϊƽ���ı��Σ������ڣ��������N�����ꣻ�������ڣ���˵�����ɣ�

���𰸡���1��y=![]() x2
x2![]() 2x+3��2��-2��3��������
2x+3��2��-2��3��������![]() 1��
1��![]() 2����
2����![]() 1��0��
1��0��
����������������1������ֱ��![]() ��
��![]() ���
���![]() ��Ľ������꣬���ô���ϵ�����������ߵĽ���ʽ��
��Ľ������꣬���ô���ϵ�����������ߵĽ���ʽ��
��2�����ݵ�C�ĺ�����Ϊm�ɵ�D��E�ĺ����궼��m�����ݽ���ʽ��ʾ�������꣬����Ǧֱ�߶�DE�ij������ù��ɶ����ã�![]() ��������֪��ʽ�ɵ�m��ֵ��
��������֪��ʽ�ɵ�m��ֵ��
��3�������������
����BCΪһ�ߣ���ͼ1��֤��![]() ��
��![]() ����
����![]() �ɵ�
�ɵ�![]()
�ڵ�BDΪ�Խ���ʱ����ͼ2��M�������ߵĶ��㣬N�ǶԳ�����x��Ľ��㣬��ʱ![]()
��⣺(1)��x=0ʱ��y=3��
��B(0,3)��
��y=0ʱ��x+3=0��
x=3��
��A(3,0)��
��A(3,0),B(0,3)����������![]() �еã�
�еã�
![]() ��ã�
��ã�![]()
�������ߵĽ���ʽΪ��![]()
(2)��CD��OA,C(m,0)��
��![]()
��![]()
��AC=m+3,CD=m+3,
�ɹ��ɶ����ã�![]()
��![]()
��![]()
![]()
(m+3)(m+2)=0��
m1=3(��),m2=2��
(3)���ڣ������������
����BCΪһ�ߣ���ͼ1����Գ�����x�ύ�ڵ�G��
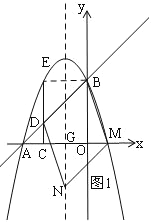
��C(2,0)��
��D(2,1),E(2,3),
��E��B���ڶԳ���Գƣ�
��BE��x�ᣬ
���ı���DNMB��ƽ���ı��Σ�
��BD=MN,BD��MN��
��![]()
���EDB�ա�GNM��
��NG=ED=2��
��N(1,2)��
�ڵ�BDΪ�Խ���ʱ����ͼ2��
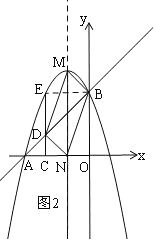
M�������ߵĶ��㣬N�ǶԳ�����x��Ľ��㣬��ʱ�ı���BMDN��ƽ���ı��Σ�
��ʱN(1,0)��
��������,��N������Ϊ(1,2)��(1,0).

 ��ְٷְټ���ϵ�д�
��ְٷְټ���ϵ�д� �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д� �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�����Ŀ��ijУ������������д��������ÿλѧ����д����39�������������������鲿��ѧ������д����������Ǹ��ݳ�������Ƶ�ͳ��ͼ��һ����
��� |
|
|
|
|
|
��ȷ���� |
|
|
|
|
|
���� | 10 | 15 | 25 |
|
|

����������Ϣ����������⣺
��1����ͳ�Ʊ��У�![]() ��
��![]() ������ȫ����ͳ��ͼ.
������ȫ����ͳ��ͼ.
��2������ͳ��ͼ����![]() ��������Ӧ��Բ�ĽǵĶ����� .
��������Ӧ��Բ�ĽǵĶ����� .
��3������У����900��ѧ���������д��ȷ�ĸ�������24����Ϊ���ϸ������������ѧУ���α�����д���ϸ��ѧ������