��Ŀ����
����Ŀ��Ϊ��������ͨ�У�ij�㳡�ƻ����½�Ϊ30�㣬�³�Ϊ60��б��AB���и��죬��б���е�D����ȥ�������壨��Ӱ��ʾ������һ��ƽ����ˮƽ��CA��ƽ̨DE��һ���µ�б��BE��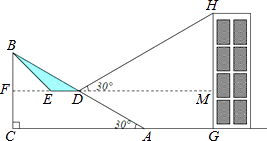
��1��������б��BE���½�Ϊ36�㣬��ƽ̨DE�ij�ԼΪ�����ף�
��2���ھ����½�A��27��Զ��G�����̳���¥��С����D������¥����H ������Ϊ30�㣬��ô��¥GH��ԼΪ�����ף������ȡ�������ο����ݣ�sin36��=0.6��cos36��=0.8��tan36��=0.7�� ![]() =1.7��
=1.7��
���𰸡�
��1���⣺������б��BE���½ǣ�����BEF��Ϊ36�㣬
���BEF=36�㣬
�ߡ�DAC=��BDF=30�㣬AD=BD=30��
��BF= ![]() BD=15��DF=15
BD=15��DF=15 ![]() ��25.98��
��25.98��
EF= ![]() =
= ![]() ��21.43
��21.43
�ʣ�DE=DF��EF=4���ף�
��2���⣺����D��DP��AC������ΪP��
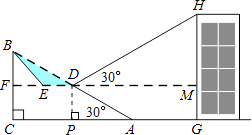
��Rt��DPA��DP= ![]() AD=
AD= ![]() ��30=15��
��30=15��
PA=ADcos30��= ![]() ��30=15
��30=15 ![]() ��
��
�ھ���DPGM�У�MG=DP=15��DM=PG=15 ![]() +27��
+27��
��Rt��DMH��
HM=DMtan30��= ![]() ����15
����15 ![]() +27��=15+9
+27��=15+9 ![]() ��
��
GH=HM+MG=15+15+9 ![]() ��45�ף�
��45�ף�
�𣺽�����GH��ԼΪ45�ף�
����������1���������⣬��֤�á�DAC=��BDF��AD=BD����Rt��BDF�У����ý�ֱ�����������BF��DF�ij���Ȼ����Rt��BEF�У������EF�ij������ɵó��𰸡�
��2������D��DP��AC������ΪP����Rt��DPA�У����DP��PA�ij����Ӷ����DM�ij�������Rt��DMH�У����ý�ֱ�����������HM�ij����������������GH�ߡ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ij����Ͷ��31500Ԫ����A��B�������Ϲ�800�䣬���ϵijɱ������ۼ����±�������λ��Ԫ/�䣩
��� | �ɱ��� | ���ۼ� |
A | 42 | 64 |
B | 36 | 52 |
��1���ó��й���A��B�������ϸ������䣿
��2��ȫ������800�����Ϲ�ӯ������Ԫ��
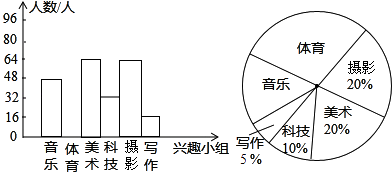
����Ŀ����ͼ������ʮ�ܲ��Լס��������˶�Ա�������������ͳ��ͼ��������涨�����ܲ��Գɼ�70������(����70��)Ϊ����.
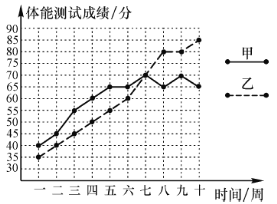
(1)�����ͼ�����ṩ����Ϣ��д�±���
ƽ���� | ��λ�� | ���ܲ��Գɼ��ϸ�������Σ� | |
�� | 65 | ||
�� | 60 |
(2)�������������ͬ�ĽǶȶ��˶�Ա���ܲ��Խ�������жϣ�������ƽ������ɼ��ϸ�Ĵ����Ƚϼ��ң��ĸ������ܲ��Գɼ��Ϻã�������ƽ��������λ���Ƚϼ��ң��ĸ������ܲ��Գɼ��Ϻã�
(3)��������ͳ��ͼ�ͳɼ��ϸ�Ĵ�����������λ�˶�Ա����ѵ����Ч���Ϻ�.