题目内容
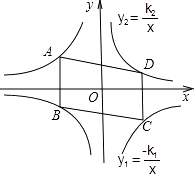
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=mx+b的图象交于A(1,3),B(n,﹣1)两点.
的图象与一次函数y=mx+b的图象交于A(1,3),B(n,﹣1)两点. 
(1)求反比例函数与一次函数的解析式;
(2)根据图象回答:当x取何值时,反比例函数的值大于一次函数的值.
【答案】
(1)解:∵A(1,3)在y= ![]() 的图象上,
的图象上,
∴k=3,∴y= ![]() .
.
又∵B(n,﹣1)在y= ![]() 的图象上,
的图象上,
∴n=﹣3,即B(﹣3,﹣1)
∴ ![]()
解得:m=1,b=2,
∴反比例函数的解析式为y= ![]() ,一次函数的解析式为y=x+2
,一次函数的解析式为y=x+2
(2)解:从图象上可知,当x<﹣3或0<x<1时,反比例函数的值大于一次函数的值
【解析】(1)反比例函数y= ![]() 的图象与一次函数y=mx+b的图象交于A(1,3),B(n,﹣1)两点,把A点坐标代入反比例函数解析式,即可求出k,得到反比例函数的解析式.将B(n,﹣1)代入反比例函数的解析式求得B点坐标,然后再把A、B点的坐标代入一次函数的解析式,利用待定系数法求出一次函数的解析式;(2)根据图象,分别在第一、三象限求出反比例函数的值大于一次函数的值时x的取值范围.
的图象与一次函数y=mx+b的图象交于A(1,3),B(n,﹣1)两点,把A点坐标代入反比例函数解析式,即可求出k,得到反比例函数的解析式.将B(n,﹣1)代入反比例函数的解析式求得B点坐标,然后再把A、B点的坐标代入一次函数的解析式,利用待定系数法求出一次函数的解析式;(2)根据图象,分别在第一、三象限求出反比例函数的值大于一次函数的值时x的取值范围.

练习册系列答案
相关题目
【题目】(本小题满分18分)某校八(1)班同学为了解2011年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
月均用水量 | 频数(户) | 频率 |
| 6 | 0.12 |
| 0.24 | |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | |
| 2 | 0.04 |
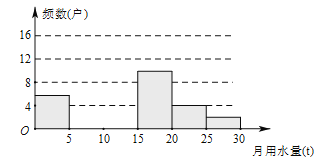
请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)若该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20 t的家庭大约有多少户?