��Ŀ����
����Ŀ��ijѧУΪ��չ����������������ƻ��ó�������3000Ԫ���ʽ���һ��������ë���ĺ�ƹ�����ģ���֪������ë���ĺ�ƹ�����ĵĵ��۱�Ϊ8:3��2�����䵥�ۺ�Ϊ130Ԫ��
��1������������ë���ĺ�ƹ�����ĵĵ��۷ֱ��Ƕ���Ԫ��
��2����Ҫ����������ë���ĺ�ƹ�����ĵ���������80������������ë���ĵ�������ƹ������������4�����ҹ���ƹ�����ĵ�����������15�������м��ֹ��������ַ���������ʹ�˷����٣������˷��Ƕ��٣�
���𰸡���1��������ë���ĺ�ƹ�����ĵĵ��۷ֱ�Ϊ80Ԫ��30Ԫ��20Ԫ����2��һ������������������һ�������٣������˷���2900Ԫ.
��������
��1���赥�۱��е�ÿһ��Ϊx����ʾ���䵥�ۣ����ݵ��ۺͿ����x�����������Ӧ���ۼ��ɣ�
��2����ϵʽΪ��ƹ�����ĵ�������15���ܼۡ�3000���������ֵ������ú��ʵ�������ĸ������ɣ�
��1����������ë���ĺ�ƹ�����ĵĵ��۱�Ϊ8�U3�U2��
�����������ǵĵ��۷ֱ�Ϊ8x��3x��2xԪ��
�����⣬��8x+3x+2x=130�����x=10��
��������ë���ĺ�ƹ�����ĵĵ��۷ֱ�Ϊ80Ԫ��30Ԫ��20Ԫ��
��2���蹺�����������Ϊy����
������ë���ĵ�����Ϊ4y��������ƹ�����ĵ�����Ϊ��80-y-4y������
�������⣬��![]()
���13��y��14��
��yȡ������
��yֻ��ȡ13��14��
��ˣ�һ��������������
����һ����y=13ʱ��������13������ë���Ĺ���52����ƹ�����Ĺ���15����
����������y=14ʱ��������14������ë���Ĺ���56����ƹ�����Ĺ���10����
����һ�������٣�Ϊ2900Ԫ.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ������С������18�֣�ijУ�ˣ�1����ͬѧΪ�˽�2011��ijС����ͥ�¾���ˮ�������������˸�С�����ּ�ͥ�������������ݽ�������������
�¾���ˮ�� | Ƶ�������� | Ƶ�� |
| 6 | 0��12 |
| 0��24 | |
| 16 | 0��32 |
| 10 | 0��20 |
| 4 | |
| 2 | 0��04 |
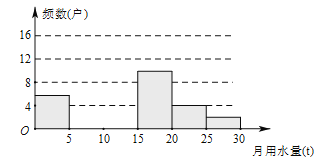
�����������⣺
��1���������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ����������
��2������С����ˮ��������15t�ļ�ͥռ�������ͥ�����İٷֱȣ�
��3������С����1000����ͥ�����ݵ������ݹ��ƣ���С���¾���ˮ������20 t�ļ�ͥ��Լ�ж��ٻ���