题目内容
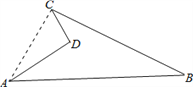
【题目】如图所示的一块地，∠ADC=90°，AD=4m，CD=3m，AB=13m，BC=12m，求这块地的面积．
【答案】这块土地的面积为24m2
【解析】连接AC，利用勾股定理可以得出三角形ACD和ABC是直角三角形，△ABC的面积减去△ACD的面积就是所求的面积．
解：连接AC．
在Rt△ACD中，AD=4，CD=3，
∴AC 2 =AD 2 +CD 2 =4 2 +3 2 =25，
又∵AC＞0，
∴AC=5．
又∵BC=12，AB=13，
∴AC 2 +BC 2 =5 2 +12 2 =169，
又∵AB 2 =169，
∴AC 2 +BC 2 =AB 2 ，
∴△ACB是直角三角形，
∴S =S △ABC -S △ADC =30-6=24m2．
“点睛”考查了直角三角形面积公式以及勾股定理的应用，作辅助线是解决本题的关键．
【题目】某市为鼓励居民节约用水，规定如下用水收费标准：每户每月的用水量不超过12吨（含12吨）时，水费按a元/吨收费；超过时，不超过12吨（含12吨）时，水费按a元/吨收费；超过时，不超过12吨的部分仍按a元/吨收费，超过的部分按b元/吨（b＞a）收费，已知该市小明家今年3月份和4月份的用水量、水费如表所示：
月份 | 用水量（立方米） | 水费（元） |
3 | 28 | 56 |
4 | 20 | 35.2 |
（1）求a，b的值；
（2）设某户1个月的用水量为x（吨），应交水费y（元），求出y与x之间的函数关系式；
（3）已知某户5月份的用水量为18吨，求该户5月份的水费．
【题目】一方有难八方支援，某市政府筹集了抗旱必需物资120吨打算运往灾区，现有甲、乙、丙三种车型供选择，每辆车的运载能力和运费如下表所示：（假设每辆车均满载）
车型 | 甲 | 乙 | 丙 |
汽车运载量（吨/辆） | 5 | 8 | 10 |
汽车运费（元/辆） | 400 | 500 | 600 |
（1）若全部物资都用甲、乙两种车型来运送，需运费8200元，问分别需甲、乙两种车型各几辆？
（2）为了节约运费，该市政府可以调用甲、乙、丙三种车型参与运送，已知它们的总辆数为16辆，你能通过列方程组的方法分别求出几种车型的辆数吗？
（3）求出那种方案的运费最省？最省是多少元．