ЬтФПФкШн
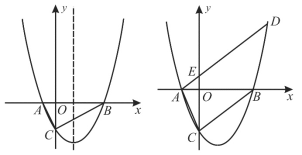
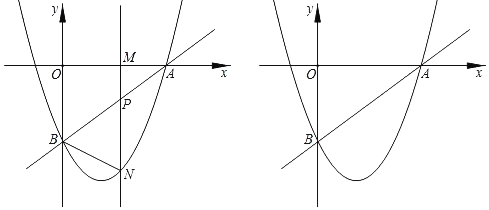
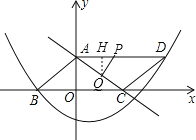
ЁОЬтФПЁПШчЭМЃЌЕуAЁЂCЗжБ№ЪЧвЛДЮКЏЪ§yЃНЉ![]() x+3ЕФЭМЯѓгыyжсЁЂxжсЕФНЛЕуЃЌЕуBгыЕуCЙигкдЕуЖдГЦЃЌЖўДЮКЏЪ§yЃН
x+3ЕФЭМЯѓгыyжсЁЂxжсЕФНЛЕуЃЌЕуBгыЕуCЙигкдЕуЖдГЦЃЌЖўДЮКЏЪ§yЃН![]() x2+bx+cЕФЭМЯѓОЙ§ЕуBЃЌЧвИУЖўДЮКЏЪ§ЭМЯѓЩЯДцдквЛЕуDЃЌЪЙЫФБпаЮABCDФмЙЙГЩЦНааЫФБпаЮЃЎ
x2+bx+cЕФЭМЯѓОЙ§ЕуBЃЌЧвИУЖўДЮКЏЪ§ЭМЯѓЩЯДцдквЛЕуDЃЌЪЙЫФБпаЮABCDФмЙЙГЩЦНааЫФБпаЮЃЎ
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉЖЏЕуPДгЕуAЕНЕуDЃЌЭЌЪБЖЏЕуQДгЕуCЕНЕуAЖМвдУПУы1ИіЕЅЮЛЕФЫйЖШдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊtУыЃЎ
ЂйЕБtЮЊКЮжЕЪБЃЌгаPQAACЃП
ЂкЕБtЮЊКЮжЕЪБЃЌЫФБпаЮPDCQЕФУцЛ§зюаЁЃПДЫЪБЫФБпаЮPDCQЕФУцЛ§ЪЧЖрЩйЃП
ЁОД№АИЁПЃЈ1ЃЉyЃН![]() x2Љ
x2Љ![]() xЉ3ЃЛЃЈ2ЃЉЂйЕБtЃН
xЉ3ЃЛЃЈ2ЃЉЂйЕБtЃН![]() УыЪБЃЌPQЁЭACЃЌЂкЕБtЃН
УыЪБЃЌPQЁЭACЃЌЂкЕБtЃН![]() ЪБЃЌЫФБпаЮPDCQЕФУцЛ§зюаЁЃЌзюаЁУцЛ§ЮЊ
ЪБЃЌЫФБпаЮPDCQЕФУцЛ§зюаЁЃЌзюаЁУцЛ§ЮЊ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЯШРћгУвЛДЮКЏЪ§ЕФНтЮіЪНШЗЖЈAЕуКЭCЕузјБъЃЌдйРћгУЕуBгыЕуCЙигкдЕуЖдГЦЕУЕНЕуBЕузјБъКЭBCЕФГЄЃЌНгзХРћгУЦНааЫФБпаЮЕФаджЪЧѓГіDЕузјБъЃЌШЛКѓАбЕуBКЭЕуDЕФзјБъДњШыЖўДЮКЏЪ§yЃН![]() x2+bx+cЕУЙигкbЁЂcЕФЗНГЬзщЃЌдйНтЗНГЬзщЧѓГіbЁЂcМДПЩЕУЕНЖўДЮКЏЪ§БэДяЪНЃЛ
x2+bx+cЕУЙигкbЁЂcЕФЗНГЬзщЃЌдйНтЗНГЬзщЧѓГіbЁЂcМДПЩЕУЕНЖўДЮКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЂйЯШРћгУЙДЙЩЖЈРэМЦЫуГіACЃН5ЃЌдйРћгУtБэЪОГіAPЃНtЃЌCQЃНtЃЌAQЃН5ЉtЃЌЕБPQЁЭACЪБПЩжЄУїЁїAPQЁзЁїCAOЃЌдђРћгУЯрЫЦБШЕУЕН![]() ЃЌНтЕУtЃН
ЃЌНтЕУtЃН![]() ЃЌШЛКѓНтЗНГЬЧѓГіtМДПЩЃЛ
ЃЌШЛКѓНтЗНГЬЧѓГіtМДПЩЃЛ
ЂкзїQHЁЭADгкHЃЌШчЭМЃЌЯШжЄУїЁїAQHЁзЁїCAOЃЌРћгУЯрЫЦБШПЩБэЪОГіQHЃН![]() ЃЈ5ЉtЃЉЃЌдйИљОнШ§НЧаЮУцЛ§ЙЋЪНЃЌРћгУSЫФБпаЮPDCQЃНSЁїACDЉSЁїAQPЕУЕНЫФБпаЮPDCQЕФУцЛ§ЃН
ЃЈ5ЉtЃЉЃЌдйИљОнШ§НЧаЮУцЛ§ЙЋЪНЃЌРћгУSЫФБпаЮPDCQЃНSЁїACDЉSЁїAQPЕУЕНЫФБпаЮPDCQЕФУцЛ§ЃН![]() t2Љ
t2Љ![]() t+12ЃЌШЛКѓИљОнЖўДЮКЏЪ§ЕФаджЪЧѓНтЃЎ
t+12ЃЌШЛКѓИљОнЖўДЮКЏЪ§ЕФаджЪЧѓНтЃЎ
НтЃКЃЈ1ЃЉЕБxЃН0ЃЌyЃНЉ![]() x+3ЃН3ЃЌдђЕуAЃЈ0ЃЌ3ЃЉЃЌ
x+3ЃН3ЃЌдђЕуAЃЈ0ЃЌ3ЃЉЃЌ
ЕБyЃН0ЃЌЉ![]() x+3ЃН0ЃЌНтЕУxЃН4ЃЌдђЕуCЃЈ4ЃЌ0ЃЉЃЌ
x+3ЃН0ЃЌНтЕУxЃН4ЃЌдђЕуCЃЈ4ЃЌ0ЃЉЃЌ
ЁпЕуBгыЕуCЙигкдЕуЖдГЦЃЌ
ЁрЕуBЃЈЉ4ЃЌ0ЃЉЃЌBCЃН8ЃЌ
ЁпЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЌ
ЁрADЁЮxжсЃЌADЃНBCЃН8ЃЌ
ЁрDЃЈ8ЃЌ3ЃЉЃЌ
НЋЕуBЃЈЉ4ЃЌ0ЃЉЃЌЕуDЃЈ8ЃЌ3ЃЉДњШыЖўДЮКЏЪ§yЃН![]() x2+bx+cЕУ
x2+bx+cЕУ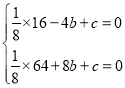 ЃЌНтЕУ
ЃЌНтЕУ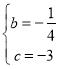 ЃЌ
ЃЌ
ЁрЖўДЮКЏЪ§БэДяЪНyЃН![]() x2Љ
x2Љ![]() xЉ3ЃЛ
xЉ3ЃЛ
ЃЈ2ЃЉЂйЁпAЃЈ0ЃЌ3ЃЉЃЌCЃЈ4ЃЌ0ЃЉЃЌ
ЁрACЃН![]() ЃН5ЃЌ
ЃН5ЃЌ
ЃЌЕБЕуPдЫЖЏСЫtУыЪБЃЌдђAPЃНtЃЌCQ
ЂкзїQHЁЭADгкHЃЌШчЭМЃЌ
ЁпЁЯHAQЃНЁЯOCAЃЌ
ЁрЁїAQHЁзЁїCAOЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌНтЕУQHЃН
ЃЌНтЕУQHЃН![]() ЃЈ5ЉtЃЉЃЌ
ЃЈ5ЉtЃЉЃЌ
ЁрSЫФБпаЮPDCQЃНSЁїACDЉSЁїAQP
ЃН![]() 38Љ
38Љ![]() t
t![]() ЃЈ5ЉtЃЉ
ЃЈ5ЉtЃЉ
ЃН![]() t2Љ
t2Љ![]() t+12
t+12
ЃН![]() ЃЈtЉ
ЃЈtЉ![]() ЃЉ2+
ЃЉ2+![]() ЃЌ
ЃЌ
ЁрЕБtЃН![]() ЪБЃЌЫФБпаЮPDCQЕФУцЛ§зюаЁЃЌзюаЁУцЛ§ЮЊ
ЪБЃЌЫФБпаЮPDCQЕФУцЛ§зюаЁЃЌзюаЁУцЛ§ЮЊ![]() ЃЎ
ЃЎ

 аЁЬьВХПЮЪБзївЕЯЕСаД№АИ
аЁЬьВХПЮЪБзївЕЯЕСаД№АИ вЛПЮЫФСЗЯЕСаД№АИ
вЛПЮЫФСЗЯЕСаД№АИ ЛЦИдаЁзДдЊТњЗжГхДЬЮЂВтбщЯЕСаД№АИ
ЛЦИдаЁзДдЊТњЗжГхДЬЮЂВтбщЯЕСаД№АИ аТИЈНЬЕМбЇЯЕСаД№АИ
аТИЈНЬЕМбЇЯЕСаД№АИ бєЙтЭЌбЇвЛЯпУћЪІШЋгХКУОэЯЕСаД№АИ
бєЙтЭЌбЇвЛЯпУћЪІШЋгХКУОэЯЕСаД№АИ