Question

【题目】如图，电信部门计划修建一条连接B、C两地电缆，测量人员在山脚A处测得B、C两处的仰角分别是37°和45°，在B处测得C处的仰角为67°．已知C地比A地髙330米（图中各点均在同一平面内），求电缆BC长至少多少米？

（精确到米，参考数据：sin37°≈，tan37°≈，sin67°≈，tan67°≈）

Answer 1

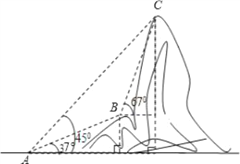
【答案】电缆BC长至少130米．

【解析】解：如图，过点C作经过点A的水平直线的垂线，垂足为点D，

CD交过点B的水平直线于点E，过点B作BF⊥AD于点F，则CD=330米，

∵∠CAD=45°∴∠ACD=45°∴AD=CD=330米，

设AF=4x，则BF=AFtan37°≈4x0.75=3x（米）FD=（330﹣4x）米，

由四边形BEDF是矩形可得：BE=FD=（330﹣4x）米，ED=BF=3x米，

∴CE=CD﹣ED=（330﹣3x）米，

在Rt△BCE中，CE=BEtan67°，∴330﹣3x=（330﹣4x）×2.4，解得x=70，

∴CE=330﹣3×70=120（米），∴BC==≈130（米）

答：电缆BC长至少130米．