��Ŀ����
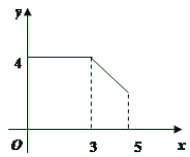
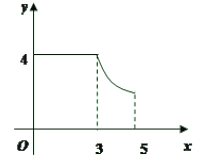
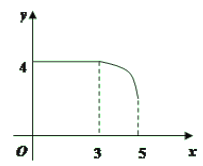
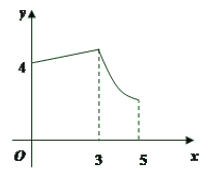
����Ŀ����ͼ��ֱ��y��![]() x+a��x�ύ�ڵ�A��4��0������y�ύ�ڵ�B��������y��
x+a��x�ύ�ڵ�A��4��0������y�ύ�ڵ�B��������y��![]() x2+bx+c������A��B����M��m��0��Ϊx����һ���㣬����M�Ҵ�ֱ��x���ֱ�߷ֱ�ֱ��AB���������ڵ�P��N��
x2+bx+c������A��B����M��m��0��Ϊx����һ���㣬����M�Ҵ�ֱ��x���ֱ�߷ֱ�ֱ��AB���������ڵ�P��N��
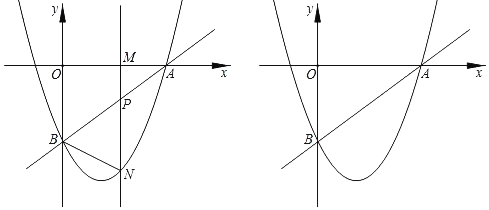
��1����գ���B������Ϊ�� ���������ߵĽ���ʽΪ�� ����
��2������M���߶�OA���˶�ʱ�������O��A�غϣ���
�ٵ�mΪ��ֵʱ���߶�PN���ֵ�������PN�����ֵ�������ʹ��BPNΪֱ��������ʱm��ֵ��
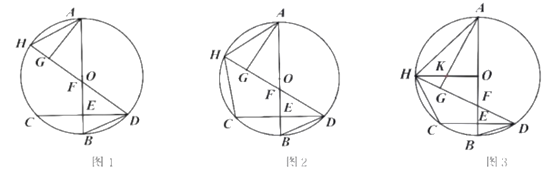
��3����������������ֻ��������N��ֱ��AB�ľ�����h����ֱ��д����ʱ�ɵ�O��B��N��P���ɵ��ı��ε������
���𰸡���1����0����3����y��![]() x2��
x2��![]() x��3����2������3����3��
x��3����2������3����3��![]() ����3��6��6+6
����3��6��6+6![]() ��6
��6![]() ��6��
��6��
��������
(1)�ѵ�A���������ֱ�߱���ʽy��![]() x+a�����a=-3���ѵ�A��B�����������κ�������ʽ��������ֵ.
x+a�����a=-3���ѵ�A��B�����������κ�������ʽ��������ֵ.
(2) �ٵ�P��m��![]() m��3������N��m��
m��3������N��m��![]() m2��
m2��![]() m��3�����PNֵ�ı���ʽ��������⣬
m��3�����PNֵ�ı���ʽ��������⣬
�ڷ֡�BNP��90������NBP��90������BPN��90������������ֱ����.
(3)����������ֻ��������N��ֱ��AD�ľ�����h,��ֻ�ܳ��֣���ABֱ���·������������N��ֱ������������һ������N����ֱ��AB�Ϸ��Ľ������������ֱ���⼴��.
�⣺��1���ѵ�A�������ֱ�߱���ʽy��![]() x+a��
x+a��
��ã�a����3����ֱ�߱���ʽΪ��y�T![]() x��3����x��0����y����3��
x��3����x��0����y����3��
���B������0����3����
����B�����������κ�������ʽ�ã�c����3��
�ѵ�A�����������κ�������ʽ�ã�![]() ��16+4b��3��0��
��16+4b��3��0��
��ã�b����![]() ��
��
�������ߵĽ���ʽΪ��y��![]() x2��
x2��![]() x��3��
x��3��
��2���١�M��m��0�����߶�OA�ϣ���MN��x�ᣬ
���P��m��![]() m��3����N��m��
m��3����N��m��![]() m2��
m2��![]() m��3����
m��3����
��PN��![]() m��3����
m��3����![]() m2��
m2��![]() m��3������
m��3������![]() ��m��2��2+3��
��m��2��2+3��
��a����![]() ��0��
��0��
�������߿������£�
�൱m��2ʱ��PN�����ֵ��3��
�ڵ���BNP��90��ʱ����N��������Ϊ��3��
��y����3���������ߵı���ʽ�ã���3��![]() m2��
m2��![]() m��3����ã�m��3��0����ȥm��0����
m��3����ã�m��3��0����ȥm��0����
��m��3��
����NBP��90��ʱ����BN��AB����ֱ�ߴ�ֱ����kֵ���Ϊ��1��
�裺ֱ��BN�ı���ʽΪ��y����![]() x+n��
x+n��
�ѵ�B�����������ʽ����ã�n����3����ֱ��BN�ı���ʽΪ��y����![]() x��3��
x��3��
����ʽ�������ߵı���ʽ��������ã�m��![]() ��0����ȥm��0����
��0����ȥm��0����
����BPN��90��ʱ������������ȥ��
�ʣ�ʹ��BPNΪֱ��������ʱm��ֵΪ3��![]() ��
��
��3����OA��4��OB��3��
��Rt��AOB��tan����![]() ����cos����
����cos����![]() ��sin����
��sin����![]() ��
��
��PM��y�ᣬ
���BPN����ABO������
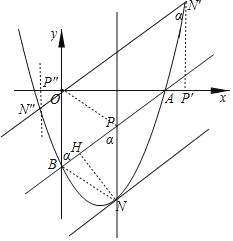
��������������ֻ��������N��ֱ��AB�ľ�����h��
��ֻ�ܳ��֣���ABֱ���·������������N��ֱ������������һ������N����ֱ��AB�Ϸ��Ľ�����������
������N��ֱ������������һ������N��
��M������Ϊ��m��0�����裺��N����Ϊ����m��n����
��n��![]() m2��
m2��![]() m��3������N��AB��ƽ���ߣ�
m��3������N��AB��ƽ���ߣ�
���N���ڵ�ֱ�߱���ʽΪ��y��![]() x+b������N������룬
x+b������N������룬
��ã���N��ֱ�߱���ʽΪ��y��![]() x+��n��
x+��n��![]() m����
m����
�������ߵı���ʽ����ʽ�����������ã�3x2��12x��12+3m��4n��0��
����144��3��4������12+3m��4n����0��
��n��![]() m2��
m2��![]() m��3������ʽ�������ã�m2��4m+4��0��
m��3������ʽ�������ã�m2��4m+4��0��
��ã�m��2�����N������Ϊ��2����![]() ����
����
��P������2����![]() ����
����
��PN��3��
��OB��3��PN��OB��
���ı���OBNPΪƽ���ı��Σ����O��ֱ��AB�ľ�����ڵ�N��ֱ��AB�ľ��룬
��������O��ABƽ�е�ֱ���������ߵĽ���Ϊ��������N�㣬����N����N����
ֱ��ON�ı���ʽΪ��y��![]() x�����ñ���ʽ����κ�������ʽ�����������ã�
x�����ñ���ʽ����κ�������ʽ�����������ã�
x2��4x��4��0����ã�x��2��2![]() ��
��
���N����N���ĺ�����ֱ�Ϊ2+2![]() ��2��2
��2��2![]() ��
��
��NH��AB��ֱ��AB�ڵ�H��
��h��NH��NPsin����![]() ��
��
��N��P����x�ᣬ��x���ڵ�P������ON��P��������ON����![]() ��
��![]() ��2+2
��2+2![]() ����
����
S�ı���OBPN��BPh��![]() ��6��
��6��
��S�ı���OBP��N����S��OP��N��+S��OBP����6+![]() ��
��
ͬ����S�ı���OBN��P����![]() ��6��
��6��
�ʣ���O��B��N��P���ɵ��ı��ε����Ϊ��6��6+6![]() ��6
��6![]() ��6��
��6��

����Ŀ����ͼ����֪y��x��x>0���ĺ�������1�и����˼���x��y�Ķ�Ӧֵ��
��1��
x | �� |
| 1 |
| 2 |
| 3 | �� |
y | �� | 6 | 3 | 2 |
|
| 1 | �� |
���Ա��и��Զ�ӦֵΪ���꣬��ͼ1��ֱ������ϵ��������㣬�ù⻬����˳������.��ͼ��֪�����������Ѿ�ѧ�������ຯ���������������ʽ����ֱ��д��![]() ��ֵ��
��ֵ��
�����һ�κ���ͼ�������ͼ���ڣ�1��3���ͣ�3��1�����㣬�ڵ�һ���������ڵ�x��ʲô��Χʱ��һ�κ�����ֵС�ڢ��к�����ֵ����ֱ��д����.