题目内容
【题目】已知四边形![]() 内接于
内接于![]() ,对角线
,对角线![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
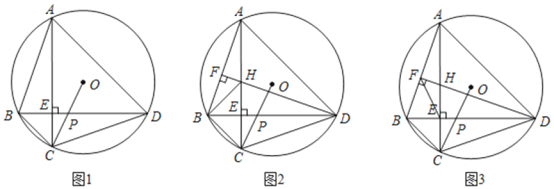
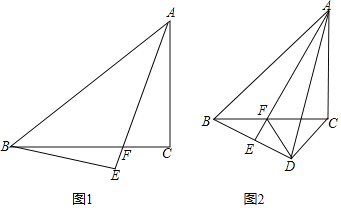
(1)如图1,求证:![]() ;
;
(2)如图2,作![]() 于
于![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
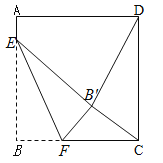
(3)在(2)的条件下,连接![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 长.
长.
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】
(1)延长CO交⊙O于K,连接DK,利用圆周角定理得到∠CDK=90°,根据AC⊥BD及圆周角定理求得∠CBD=∠CKD,即可求出结论;
(2)根据垂直的定义及圆周角定理得到∠BDC=∠BDF,得到DB垂直平分CH,即可证得结论;
(3)作EQ⊥EF交FD于Q,ON⊥AC于N,OM⊥BD于M ,先证△AED与△BEC都为等腰直角三角形,根据 △AEF≌△DEQ求出![]() ,勾股定理得AD=
,勾股定理得AD=![]() ,得到AE=ED=12,再利用BE:DE=1:3及勾股定理求出OC即可.
,得到AE=ED=12,再利用BE:DE=1:3及勾股定理求出OC即可.
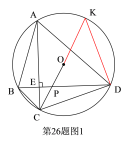
(1)解:延长CO交⊙O于K,连接DK.
∵CK为⊙O直径,
∴∠CDK=90°,
∴∠OCD+∠CKD=90°,
∵AC⊥BD于E ,
∴∠BEC=90°,
∴∠ACB+∠CBD=90°,
∵∠CBD=∠CKD,
∴∠ACB=∠OCD ;
(2)∵DF⊥AB于F,
∴∠DFB=90°,
∵AC⊥BD于E,
∴∠AEB=90°,
∴∠BAC+∠DBF=90°,
∴∠BDF+∠DBF=90°,
∴∠BDF=∠BAC,
∵∠BAC=∠BDC,
∴∠BDC=∠BDF,
∴∠DHC=∠DCH,
∴DB垂直平分CH,
∴BH=BC;
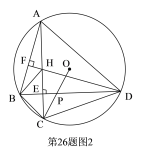
(3)作EQ⊥EF交FD于Q,ON⊥AC于N,OM⊥BD于M ,
∵BC∥AD,
∴∠BCA=∠DAC,
∵∠BCA=∠ADB,
∴∠DAC=∠ADB,
∴△AED与△BEC都为等腰直角三角形,
∵△AEF≌△DEQ,
∴AF=QD=![]() ,EF=EQ=
,EF=EQ=![]() ,
,
∴FQ=![]() ,
,
∴![]() ,勾股定理得AD=
,勾股定理得AD=![]() ,
,
∴AE=ED=12,
∵BE:DE=1:3,
∴BE=CE=4,
∴BD=AC=16,
∴BM=CN=8,
∴OM=EN=4,
∴ON=EM=4,
∴OC=![]() .
.


 名校课堂系列答案
名校课堂系列答案【题目】益马高速通车后,将桃江马迹塘的农产品运往益阳的运输成本大大降低。马迹塘一农户需要将A,B两种农产品定期运往益阳某加工厂,每次运输A,B产品的件数不变,原来每运一次的运费是1200元,现在每运一次的运费比原来减少了300元,A,B两种产品原来的运费和现在的运费(单位:元∕件)如下表所示:
品种 | A | B |
原来的运费 | 45 | 25 |
现在的运费 | 30 | 20 |
(1)求每次运输的农产品中A,B产品各有多少件?
(2)由于该农户诚实守信,产品质量好,加工厂决定提高该农户的供货量,每次运送的总件数增加8件,但总件数中B产品的件数不得超过A产品件数的2倍,问产品件数增加后,每次运费最少需要多少元?
【题目】为争创文明城市,我市交警部门在全市范围开展了安全使用电瓶车专项宣传活动.在活动前和活动后分别随机抽取了部分使用电瓶车的市民,就骑电瓶车戴安全帽情况进行问卷调查,并将两次收集的数据制成如下统计图表.

类别 | 人数 | 百分比 |
A | 68 | 6.8% |
B | 245 | b% |
C | a | 51% |
D | 177 | 17.7% |
总计 | c | 100% |
根据以上提供的信息解决下列问题:
(1)a= ,b= c=
(2)若我市约有30万人使用电瓶车,请分别计算活动前和活动后全市骑电瓶车“都不戴”安全帽的人数.
(3)经过某十字路口,汽车无法继续直行只可左转或右转,电动车不受限制,现有一辆汽车和一辆电动车同时到达该路口,用画树状图或列表的方法求汽车和电动车都向左转的概率.
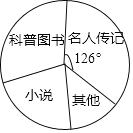
【题目】2018年东营市教育局在全市中小学开展了“情系疏勒书香援疆”捐书活动,200多所学校的师生踊跃参与,向新疆疏勒县中小学共捐赠爱心图书28.5万余本.某学校学生社团对本校九年级学生所捐图书进行统计,根据收集的数据绘制了下面不完整的统计图表.请你根据统计图表中所提供的信息解答下列问题:
图书种类 | 频数(本) | 频率 |
名人传记 | 175 | a |
科普图书 | b | 0.30 |
小说 | 110 | c |
其他 | 65 | d |
(1)求该校九年级共捐书多少本;
(2)统计表中的a= ,b= ,c= ,d= ;
(3)若该校共捐书1500本,请估计“科普图书”和“小说”一共多少本;
(4)该社团3名成员各捐书1本,分别是1本“名人传记”,1本“科普图书”,1本“小说”,要从这3人中任选2人为受赠者写一份自己所捐图书的简介,请用列表法或树状图求选出的2人恰好1人捐“名人传记”,1人捐“科普图书”的概率.