题目内容
【题目】已知,如图,在直角三角形ABC中,∠ACB=900,D是AB上一点,且∠ACD=∠B
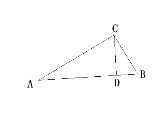
(1)判断△ACD的形状?并说明理由。
(2)你在证明你的结论过程中应用了哪一对互逆的真命题?
【答案】答:△ACD是直角三角形 理由:可证△ACD∽△ABC ,对应角∠ACD=∠ACB=90°所以CD⊥AB
互逆的真命题:两个三角形相似,对应角相等。
两个直角三角形对应角相等,则两个三角形相似。
【解析】
试题分析:依题意知∠ACD=∠B,且∠A =∠A,可得△ACD∽△ABC。因为∠ACB=900
所以对应角∠ACD=∠ACB=90°。则△ACD是直角三角形
(2)互逆的真命题:两个三角形相似,对应角相等。
两个直角三角形对应角相等,则两个三角形相似。

练习册系列答案
相关题目