题目内容
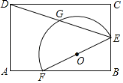
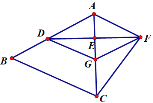
【题目】如图，AB=BC，点D为边AB的中点，点G为AC边的中点，AF∥BC且AD=AF．点E为DF与AC的交点，若AB=6，AE=1，则CF的长为___．
【答案】
【解析】
先根据中位线定理求出DG=3，DG ∥BC，进而证明四边形ADGF是菱形，求出EF=
，再根据勾股定理求出 CF=．
解：∵AB=BC，AB=6，
∴BC=6，
∵点D为边AB的中点，点G为AC边的中点，
∴DG是△ABC中位线，AD=
AB=3，
∴DG=BC=3，DG∥BC，
∵AF∥BC,
∴AF∥DG,
∵ AD=AF，
∴AF=AD=3,
∵AF=DG=3，
∴四边形ADGF是平行四边形，
∵ AD=AF，
∴平行四边形ADGF是菱形，
∴AG⊥DF,AG=2AE=2,
∴AC=2AG=4,
∴CE=3,
∵在Rt△AEF中，
，
∴ 在Rt△CEF中，
，
故答案为： ．
练习册系列答案
相关题目
