Question

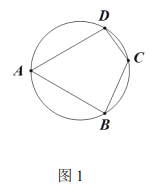
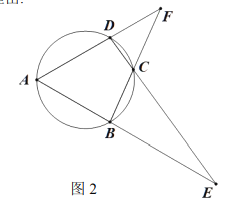
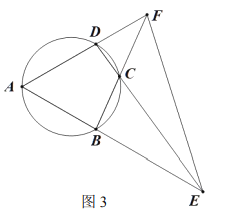
【题目】如图，点A在以BC为直径的⊙O上，连接AB、AC，点H为AB的中点．过点H的弦DE⊥BC于点F，连接CD、CH．

（1）求证：AB2=2BC·BF

（2）取AC的中点G，连接HG，过点D作线段DI与AC交于点J，与HJ的延长线交于点I．若AB=AG=4，求DJ的长．

Answer 1

【答案】（1）证明见解析；（2）

【解析】

（1）直接证明△BFH∽△BAC，得到=，而BH= ，即可得到结论；

（2）先由cos∠FBH==得到BF=，再由勾股定理及线段的和差关系得到DH= HG=，再由tan∠HDI==得到HI=，从而得到GI，DI，OI的值，又易得△OCJ∽△IGJ，得到=，从而得到关键关系：，进而根据DJ=OD+OJ得解．

解：（1）证明：∵BC为⊙O的直径，DE⊥BC

∴∠BFH=∠BAC=90°

∵∠FBH=∠ABC, 点H为AB的中点

∴△BFH∽△BAC，BH=

即=即=BC·BF

AB2=2BC·BF

（2）∵点H为AB的中点，点G为AC的中点

∴AH=BH===2，AC=2AG=8，HG, HG

∵∠BFH=∠BAC=90°∴BC==，HG=，∠BFH=∠DHI=90°

∴cos∠FBH==

∴=

∴BF=

∴Rt△BFH中：由勾股定理可得：FH==

∵⊙O的直径为 ∴OB=OC=， OF=OB - BF=-=

∵∠OFD=∠BFH=90°

∴DF==，DH=DF+FH==HG

∵tan∠HDI====即HI=， IG=HI - HG=-=

∴Rt△DHI中：由勾股定理可得：DI==， OI=DI - OD=-=

∵HG∥AC

∴△OCJ∽△IGJ

∴=

∴，

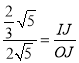∴OJ=3IJ

∴

∴DJ=OD+OJ=+=

∴DJ的长为