题目内容
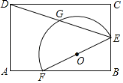
【题目】如图,矩形ABCD中,AB=3,BC=2,E为BC的中点,AF=1,以EF为直径的半圆与DE交于点G,则劣弧![]() 的长为_____.
的长为_____.
【答案】![]()
【解析】
连接OG,DF,根据勾股定理分别求出DF、EF,证明Rt△DAF≌Rt△FBE,求出∠DFE=90°,得到∠GOE=90°,根据弧长公式计算即可.
连接OG,DF,

∵BC=2,E为BC的中点,
∴BE=EC=1,
∵AB=3,AF=1,
∴BF=2,
由勾股定理得,DF=![]() ,EF=
,EF=![]() =
=![]() ,
,
∴DF=EF,
在Rt△DAF和Rt△FBE中,
![]() ,
,
∴Rt△DAF≌Rt△FBE(HL)
∴∠ADF=∠BFE,
∵∠ADF+∠AFD=90°,
∴∠BFE+∠AFD=90°,即∠DFE=90°,
∵FD=FE,
∴∠FED=45°,
∵OG=OE,
∴∠GOE=90°,
∴劣弧![]() 的长=
的长=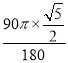 =
=![]() π,
π,
故答案为:![]() π.
π.

练习册系列答案
相关题目