题目内容
【题目】已知:![]() 是
是![]() 的直径,
的直径,![]() 的延长线上有一点
的延长线上有一点![]() ,
,![]() 是
是![]() 的切线,切点为
的切线,切点为![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .
.
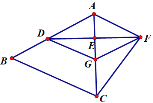
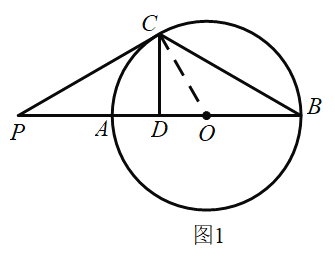
(1)如图1,求证:![]() ;
;
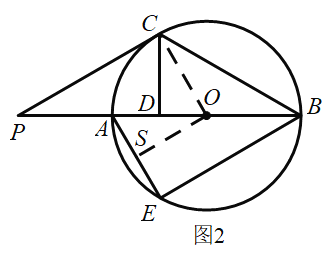
(2)如图2,![]() 是
是![]() 上的点,连接
上的点,连接![]() 、
、![]() ,若
,若![]() ,
,
求证:![]() ;
;
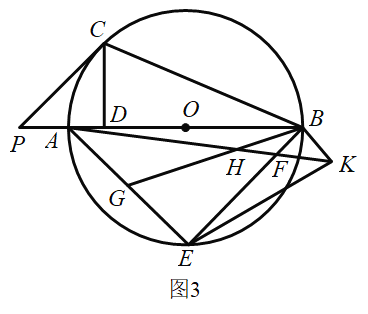
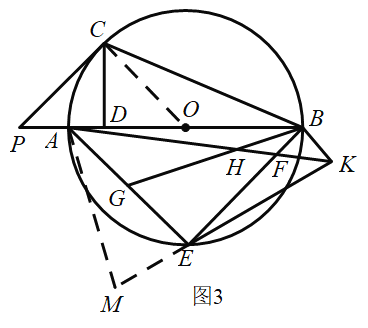
(3)如图3,在(2)的条件下,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,连接
上,连接![]() 和
和![]() 相交于点
相交于点![]() ,延长
,延长![]() 到点
到点![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.


【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)连接![]() ,由
,由![]() 是
是![]() 的切线,
的切线,![]() 可知
可知![]() ,
,![]() ,然后通过直角三角形锐角互余和同弧所对的圆心角是圆周角的二倍即可得到答案;
,然后通过直角三角形锐角互余和同弧所对的圆心角是圆周角的二倍即可得到答案;
(2)连接![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,可知
,可知![]() ,
,![]() ,设
,设![]() ,
,![]() ,得到
,得到![]() ,然后通过角度关系得到
,然后通过角度关系得到![]() ,从而可证
,从而可证![]() ,通过对应边相等即可得到结论;
,通过对应边相等即可得到结论;
(3)设![]() ,通过条件推导出
,通过条件推导出![]() ,延长
,延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() ,通过
,通过![]() 和角度关系可得到
和角度关系可得到![]() ,设
,设![]() ,则
,则![]() ,利用勾股定理求出
,利用勾股定理求出![]() ,最后证出
,最后证出![]() 为等腰直角三角形,即得到
为等腰直角三角形,即得到![]() .
.
(1)证明:如图1,连接![]() ,
,
∵![]() 是
是![]() 的切线,
的切线,
∴![]() ,
,
∴![]()
∵![]() ,
,
∴![]()
∵![]() ,
,![]()
∴![]()
∵![]() 和
和![]() 是弧
是弧![]() 所对的圆心角和圆周角
所对的圆心角和圆周角
∴![]()
∴![]()
(2)证明:如图2,连接![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
∴![]() ,
,![]()
∵![]() 是
是![]() 的直径,
的直径,
∴![]()
设![]() ,
,![]()
∵![]()
∴![]() ,即
,即![]()
∵![]() ,
,
∴![]()
∴![]()
∵![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∴![]()
(3)解:如图3,设![]() ,
,
∵![]() ,
,
∴![]()
∵![]() ,
,
∴![]()
∵![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∴![]()
∵![]() ,
,
∴![]()
延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() ,
,
∵![]() ,
,![]()
∴![]()
∴![]() ,
,![]()
∵![]()
![]()
∴![]()
∴![]() ,
,
∴![]()
设![]() ,则
,则![]()
在![]() 中,
中,![]()
在![]() 中,
中,![]()
![]()
∴![]()
![]()
∴![]()
在![]() 中,
中,![]()
连接![]() ,∵
,∵![]() ,
,![]()
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]() 为等腰直角三角形
为等腰直角三角形
∴![]()

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目