Question

【题目】（2019秋潮阳区校级月考）已知：二次函数y＝x2+bx+c的图象与x轴交于A，B两点，其中A点坐标为(﹣3，0)，与y轴交于点C，点D(﹣2，﹣3)在抛物线上．

（1）求抛物线的解析式；

（2）抛物线的对称轴上有一动点P，求△PAD周长的最小值；

（3）抛物线的对称轴上有一动点M，当△MAD是等腰三角形时，直接写出M点坐标．

Answer 1

【答案】（1）y＝x2+2x﹣3；（2）3；（3）点M坐标为：(﹣1，﹣1)或(﹣1，)或(﹣1，)或(﹣1，0)

【解析】

（1）将点A、D的坐标代入抛物线表达式，即可求解；

（2）点A关于函数对称轴的对称点为点B，连接PD交函数对称轴与点P，则点P为所求点，即可求解；

（3）分AM＝DM、AM＝AD、DM＝AD三种情况，分别求解即可．

（1）将点A、D的坐标代入抛物线表达式得：，解得：，

抛物线的表达式为：y＝x2+2x﹣3；

（2）y＝x2+2x﹣3，令y＝0，则x＝﹣3或1，令x＝0，则y＝﹣3，

故点B、C的坐标分别为：（1，0）、（0，﹣3）；

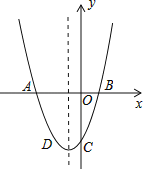
函数的对称轴为：x＝﹣1，

点A关于函数对称轴的对称点为点B，连接PD交函数对称轴与点P，则点P为所求点，

将点D、B的坐标代入一次函数表达式：y＝kx+b得：，解得：，

故BD的函数表达式为：y＝x﹣1，

当x＝﹣1时，y＝﹣2，即点P（﹣1，﹣2），

△PAD周长的最小值＝PA+PD+AD＝BD+AD3；

（3）设点M（﹣1，m），点A、D的坐标分别为：（﹣3，0）、（﹣2，﹣3），

则AM2＝4+m2，DM2＝1+（m+3）2，AD2＝1+9＝10，

当AM＝DM时，4+m2＝1+（m+3）2，解得：m＝﹣1；

当AM＝AD时，同理可得：m或；

当DM＝AD时，同理可得：m＝0或﹣6（舍去﹣6）；

综上，点M坐标为：（﹣1，﹣1）或（﹣1，）或（﹣1，）或（﹣1，0）．