题目内容
在平面直角坐标系中,现将一块等腰直角三角板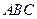 放在第二象限,斜靠在两坐标轴上,且点
放在第二象限,斜靠在两坐标轴上,且点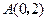 ,点
,点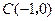 ,如图所示:抛物线
,如图所示:抛物线 经过点
经过点 。
。

(1)求点 的坐标;
的坐标;
(2)求抛物线的解析式;
(3)在抛物线上是否还存在点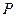 (点
(点 除外),使
除外),使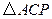 仍然是以
仍然是以 为直角边的等腰直角三角形?若存在,求所有点
为直角边的等腰直角三角形?若存在,求所有点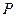 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
 放在第二象限,斜靠在两坐标轴上,且点
放在第二象限,斜靠在两坐标轴上,且点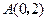 ,点
,点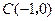 ,如图所示:抛物线
,如图所示:抛物线 经过点
经过点 。
。
(1)求点
 的坐标;
的坐标;(2)求抛物线的解析式;
(3)在抛物线上是否还存在点
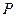 (点
(点 除外),使
除外),使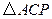 仍然是以
仍然是以 为直角边的等腰直角三角形?若存在,求所有点
为直角边的等腰直角三角形?若存在,求所有点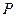 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。(1)
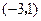
(2)
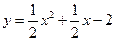
(3)点
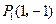 与点
与点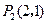 都在抛物线
都在抛物线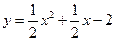 上
上解:(1)过点 作
作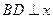 轴,垂足为
轴,垂足为 ,
,
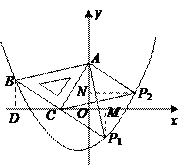

 ;
;
又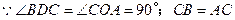 ,
,
 ,……(2分)
,……(2分)
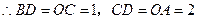
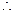 点
点 的坐标为
的坐标为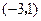 ;……(2分)
;……(2分)
(2)抛物线 经过点
经过点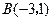 ,则得到
,则得到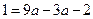 ,
,
解得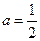 ,
,
所以抛物线的解析式为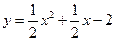 ;……(2分)
;……(2分)
(3)假设存在点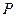 ,使得
,使得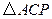 仍然是以
仍然是以 为直角边的等腰直角三角形:
为直角边的等腰直角三角形:
 若以点
若以点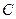 为直角顶点;
为直角顶点;
则延长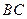 至点
至点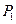 ,使得
,使得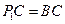 ,得到等腰直角三角形
,得到等腰直角三角形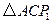 ,
,
过点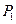 作
作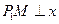 轴,
轴,
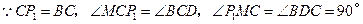 ;
;
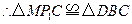
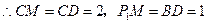 ,可求得点
,可求得点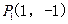 ; ……(3分)
; ……(3分)
 若以点
若以点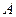 为直角顶点;
为直角顶点;
则过点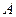 作
作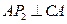 ,且使得
,且使得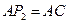 ,得到等腰直角三角形
,得到等腰直角三角形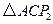 ,
,
过点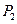 作
作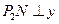 轴,同理可证
轴,同理可证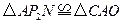 ;
;
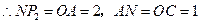 ,可求得点
,可求得点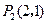 ;
;
经检验,点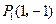 与点
与点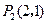 都在抛物线
都在抛物线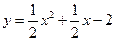 上。……(3分)
上。……(3分)
 作
作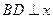 轴,垂足为
轴,垂足为 ,
,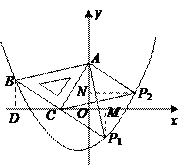

 ;
; 又
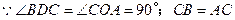 ,
, ,……(2分)
,……(2分)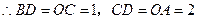
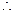 点
点 的坐标为
的坐标为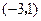 ;……(2分)
;……(2分)(2)抛物线
 经过点
经过点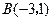 ,则得到
,则得到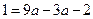 ,
, 解得
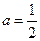 ,
,所以抛物线的解析式为
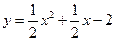 ;……(2分)
;……(2分)(3)假设存在点
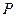 ,使得
,使得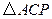 仍然是以
仍然是以 为直角边的等腰直角三角形:
为直角边的等腰直角三角形: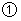 若以点
若以点 为直角顶点;
为直角顶点;则延长
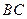 至点
至点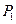 ,使得
,使得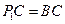 ,得到等腰直角三角形
,得到等腰直角三角形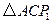 ,
,过点
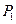 作
作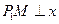 轴,
轴,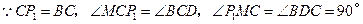 ;
;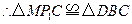
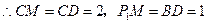 ,可求得点
,可求得点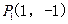 ; ……(3分)
; ……(3分) 若以点
若以点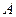 为直角顶点;
为直角顶点;则过点
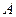 作
作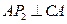 ,且使得
,且使得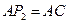 ,得到等腰直角三角形
,得到等腰直角三角形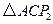 ,
,过点
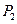 作
作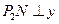 轴,同理可证
轴,同理可证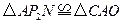 ;
;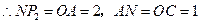 ,可求得点
,可求得点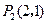 ;
;经检验,点
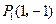 与点
与点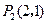 都在抛物线
都在抛物线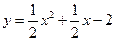 上。……(3分)
上。……(3分)
练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目

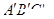 (不写
(不写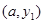 、
、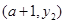 在直线
在直线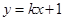 上,且
上,且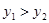 ,则该直线所经过的象限是
,则该直线所经过的象限是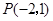 关于
关于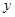 轴的对称点的坐标为
轴的对称点的坐标为 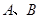 对应的数分别为2,
对应的数分别为2,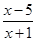 ,且
,且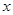 的值为___________.
的值为___________.