��Ŀ����
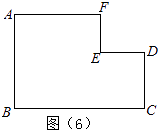
����Ŀ����֪����ABC�ǵ���ֱ�������Σ�����P��б��AB���ڵ�ֱ���ϣ���PCΪֱ�DZ�������ֱ��������PCQ�����С�PCQ=90�㣬̽��������������⣺ 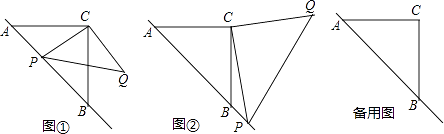
��1����ͼ�٣�����P���߶�AB�ϣ���AC=1+ ![]() ��PA=
��PA= ![]() ���� ���߶�PB= �� PC=��
���� ���߶�PB= �� PC=��
�ڲ��룺PA2 �� PB2 �� PQ2����֮���������ϵΪ��
��2����ͼ�ڣ�����P��AB���ӳ����ϣ��ڣ�1����������Ľ�����Ȼ��������������ͼ�ڸ���֤�����̣�
��3��������P���� ![]() =
= ![]() ����
���� ![]() ��ֵ������ʾ�������ñ���ͼ����̽��
��ֵ������ʾ�������ñ���ͼ����̽��
���𰸡�
��1��![]() ��2��?PA2+PB2=PQ2
��2��?PA2+PB2=PQ2
��2���⣺��ͼ�ڣ�����C��CD��AB������ΪD��

�ߡ�ACBΪ����ֱ�������Σ�CD��AB��
��CD=AD=DB��
��AP2=��AD+PD��2=��DC+PD��2=CD2+2DCPD+PD2��
PB2=��DP��BD��2=��PD��DC��2=DC2��2DCPD+PD2��
��AP2+BP2=2CD2+2PD2��
����Rt��PCD�У��ɹ��ɶ�����֪��PC2=DC2+PD2��
��AP2+BP2=2PC2��
�ߡ�CPQΪ����ֱ�������Σ�
��2PC2=PQ2��
��AP2+BP2=PQ2
��3���⣺��ͼ�ۣ�����C��CD��AB������ΪD��
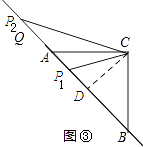
�� ����Pλ�ڵ�P1��ʱ��
�� ![]() ��
��
�� ![]() ��
��
�� ![]() ��
��
��Rt��CP1D�У��ɹ��ɶ����ã� ![]() =
= ![]() =
= ![]() DC��
DC��
��Rt��ACD�У��ɹ��ɶ����ã�AC= ![]() =
= ![]() =
= ![]() DC��
DC��
�� ![]() =
= ![]() ��
��
�ڵ���Pλ�ڵ�P2��ʱ��
�� ![]() =
= ![]() ��
��
�� ![]() ��
��
��Rt��CP2D�У��ɹ��ɶ����ã� ![]() =
= ![]() =
= ![]() ��
��
��Rt��ACD�У��ɹ��ɶ����ã�AC= ![]() =
= ![]() =
= ![]() DC��
DC��
�� ![]() ��
��
���������� ![]() �ı�ֵΪ
�ı�ֵΪ ![]() ��
�� ![]()
���������⣺��1����ͼ�٣� 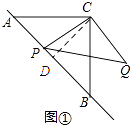
�� ��ABC�ǵ���ֱֱ�������Σ�AC=1+ ![]()
��AB= ![]() =
= ![]() =
= ![]() +
+ ![]() ��
��
��PA= ![]() ��
��
��PB= ![]() ��
��
��CD��AB��D����AD=CD= ![]() ��
��
��PD=AD��PA= ![]() ��
��
��Rt��PCD��PC= ![]() =2��
=2��
�ʴ�Ϊ�� ![]() ��2��
��2��
����ͼ1��
�ߡ�ACBΪ����ֱ�������Σ�CD��AB��
��CD=AD=DB��
��AP2=��AD��PD��2=��DC��PD��2=DC2��2DCPD+PD2 �� PB2=��DB+PD��2=��DC+DP��2=CD2+2DCPD+PD2
��AP2+BP2=2CD2+2PD2 ��
����Rt��PCD�У��ɹ��ɶ�����֪��PC2=DC2+PD2 ��
��AP2+BP2=2PC2 ��
�ߡ�CPQΪ����ֱ�������Σ�
��2PC2=PQ2 ��
��AP2+BP2=PQ2
��1�����ڵ���ֱ��������ACB�У��ɹ��ɶ��������AB�ij���Ȼ�����PA�ij��������PB�ij�������C��CD��AB������ΪD���Ӷ������CD��PD�ij���Ȼ����Rt������CDP�����ݹ��ɶ��������PC�ij����ڡ�ACBΪ����ֱ�������Σ�CD��AB���Ӷ�����ã�CD=AD=DB��Ȼ�����AP=DC��PD��PB=DC+PD����֤��AP2+BP2=2PC2 �� ��Ϊ��Rt��PCQ�У�PQ2=2CP2 �� ���Կɵó�AP2+BP2=PQ2�Ľ��ۣ���2������C��CD��AB������ΪD����AP=��AD+PD��=��DC+PD����PB=��DP��BD��=��PD��DC������֤��AP2+BP2=2PC2 �� ��Ϊ��Rt��PCQ�У�PQ2=2CP2 �� ���Կɵó�AP2+BP2=PQ2�Ľ��ۣ���3�����ݵ�P���ڵ�λ�û���ͼ�Σ�Ȼ��������Ŀ�еı�ֵ��ϵ���PD�ij����ú���CD��ʽ�ӱ�ʾ����Ȼ����Rt��ACP��Rt��DCP���ɹ��ɶ������AC��PC�ij��ȼ��ɣ�

 �ƸԴ��ž�ϵ�д�
�ƸԴ��ž�ϵ�д�����Ŀ��Word�ı��е�ͼ�Σ���ͼ�θ�ʽ�д�С�˵�����ʾ��ͼ�εľ��Ը߶Ⱥ;��Կ��ȣ�ͬһ��ͼ��������÷���ı仯������ʾ�ľ��Ը߶Ⱥ;��Կ���Ҳ��֮�仯����ͼ�١��ڡ�����ͬһ����������������ͬ�ı�ˮƽ����ʱ����������ʾ�ľ��Ը߶Ⱥ;��Կ������±������С�ABC����֪AB=AC�������Եױ�BCˮƽ����ʱ����ͼ�ܣ���������ʾ�ľ��Ը߶Ⱥ;��Կ������±�����ô����ABC����ABˮƽ����ʱ����ͼ�ݣ���������ʾ�ľ��Ը߶Ⱥ;��Կ��ȷֱ��ǣ� �� 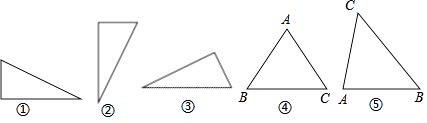
ͼ�� | ͼ�� | ͼ�� | ͼ�� | ͼ�� | ͼ�� |
���Ը߶� | 1.50 | 2.00 | 1.20 | 2.40 | �� |
���Կ��� | 2.00 | 1.50 | 2.50 | 3.60 | �� |
A.3.60��2.40
B.2.56��3.00
C.2.56��2.88
D.2.88��3.00
����Ŀ��Ϊ�˽������6000�����꼶ѧ��Ӣ�����Գɼ�����������������ȡ�˲���ѧ���ijɼ�������30�֣��÷־�Ϊ���������Ƴ��±���
�����Σ�x�֣� | x��10 | 11��x��15 | 16��x��20 | 21��x��25 | 26��x��30 |
�� �� | 10 | 15 | 35 | 112 | 128 |
��1�����γ������鹲��ȡ����ѧ����
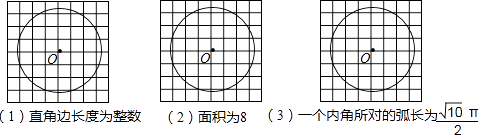
��2����������ͳ��ͼ��ʾͳ�ƽ�����������Ϊx��10����������Ӧ���ε�Բ�Ľ�Ϊ�㣻
��3��ѧ��Ӣ�����Գɼ�����������11��x��15�ķ������ڣ�����ᡱ���ᡱ��
��4������26�����ϣ���26����Ϊ���㣬����Ƹ������꼶�����ɼ�Ϊ�����������