题目内容
【题目】如图,过锐角△ABC的顶点A作DE∥BC,AB恰好平分∠DAC,AF平分∠EAC交BC的延长线于点F.在AF上取点M,使得AM= ![]() AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是
AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是 ![]() ,则
,则 ![]() 的值是 .
的值是 . 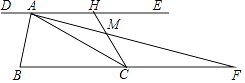
【答案】8﹣ ![]()
【解析】解:过点H作HG⊥AC于点G, ∵AF平分∠CAE,DE∥BF,
∴∠HAF=∠AFC=∠CAF,
∴AC=CF=2,
∵AM= ![]() AF,
AF,
∴ ![]() =
= ![]() ,
,
∵DE∥CF,
∴△AHM∽△FCM,
∴ ![]() =
= ![]() ,
,
∴AH=1,
设△AHM中,AH边上的高为m,
△FCM中CF边上的高为n,
∴ ![]() =
= ![]() =
= ![]() ,
,
∵△AMH的面积为: ![]() ,
,
∴ ![]() =
= ![]() AHm
AHm
∴m= ![]() ,
,
∴n= ![]() ,
,
设△AHC的面积为S,
∴ ![]() =
= ![]() =3,
=3,
∴S=3S△AHM= ![]() ,
,
∴ ![]() ACHG=
ACHG= ![]() ,
,
∴HG= ![]() ,
,
∴由勾股定理可知:AG= ![]() ,
,
∴CG=AC﹣AG=2﹣ ![]()
∴ ![]() =
= ![]() =8﹣
=8﹣ ![]()
所以答案是:8﹣ ![]()
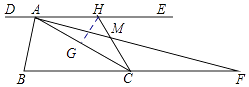
【考点精析】本题主要考查了相似三角形的判定与性质和解直角三角形的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目