题目内容
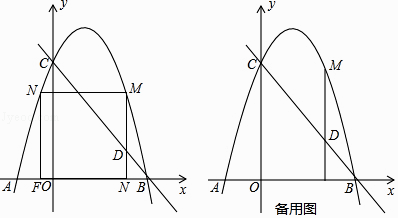
【题目】已知:Rt△EFP和矩形ABCD如图①摆放(点P与点B重合),点F,B(P),C在同一直线上,AB=EF=6cm,BC=FP=8cm,∠EFP=90°,如图②,△EFP从图①的位置出发,沿BC方向匀速运动,速度为1cm/s,EP与AB交于点G;同时,点Q从点C出发,沿CD方向匀速运动,速度为1cm/s.过点Q作QM⊥BD,垂足为H,交AD于点M,连接AF,FQ,当点Q停止运动时,△EFQ也停止运动.设运动时间为t(s)(0<t<6),解答下列问题:
(1)当t为何值时,PQ∥BD?
(2)设五边形AFPQM的面积为y(cm2),求y与t之间的函数关系式;
(3)在运动过程中,是否存在某一时刻t,使S五边形AFPQM:S矩形ABCD=9:8?若存在,求出t的值;若不存在,请说明理由.
(4)在运动过程中,是否存在某一时刻t,使点M在线段PG的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.
【答案】
(1)
解:如图1中,

当PQ∥BD时, ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴t= ![]() ,
,
∴t= ![]() s时,PQ∥BD.
s时,PQ∥BD.
(2)
解:如图2中,
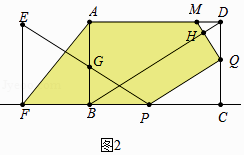
当0<t<6时,S五边形AFPQM=S梯形AFCD﹣S△DMQ﹣S△PQC
= ![]() (8+8﹣t+8)6﹣
(8+8﹣t+8)6﹣ ![]() (6﹣t)
(6﹣t) ![]() (6﹣t)﹣
(6﹣t)﹣ ![]() (8﹣t)t
(8﹣t)t
= ![]() t2﹣
t2﹣ ![]() t+
t+ ![]() .
.
(3)
解:如图2中,

假设存在,则有( ![]() t2﹣
t2﹣ ![]() t+
t+ ![]() .):48=9:8,
.):48=9:8,
解得t=2或18(舍弃),
∴t=2s时,S五边形AFPQM:S矩形ABCD=9:8.
(4)
解:存在.
理由:如图3中,连接MG、MP,作MK⊥BC于K.
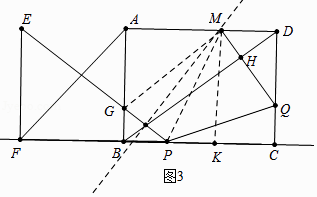
易知:AG=6﹣ ![]() t.DQ=6﹣t,DM=KC=
t.DQ=6﹣t,DM=KC= ![]() (6﹣t),PK=8﹣t﹣
(6﹣t),PK=8﹣t﹣ ![]() (6﹣t),MK=CD=6,
(6﹣t),MK=CD=6,
∵点M在PG的垂直平分线上,
∴MG=MP,
∴AG2+AM2=PK2+MK2,
∴(6﹣ ![]() t)2+[8﹣
t)2+[8﹣ ![]() (6﹣t)]2=62+[8﹣t﹣
(6﹣t)]2=62+[8﹣t﹣ ![]() (6﹣t)]2,
(6﹣t)]2,
解得t= ![]() 或0(舍弃),
或0(舍弃),
∴t= ![]() s时,点M在线段PG的垂直平分线上
s时,点M在线段PG的垂直平分线上
【解析】(1)如图1中,当PQ∥BD时, ![]() =
= ![]() ,可得
,可得 ![]() =
= ![]() ,解方程即可;(2)如图2中,当0<t<6时,S五边形AFPQM=S梯形AFCD﹣S△DMQ﹣S△PQC , 由此计算即可解决问题;(3)假设存在,根据题意列出方程即可解决问题;(4)如图3中,连接MG、MP,作MK⊥BC于K.理由勾股定理,根据MG=MP,列出方程即可解决问题;
,解方程即可;(2)如图2中,当0<t<6时,S五边形AFPQM=S梯形AFCD﹣S△DMQ﹣S△PQC , 由此计算即可解决问题;(3)假设存在,根据题意列出方程即可解决问题;(4)如图3中,连接MG、MP,作MK⊥BC于K.理由勾股定理,根据MG=MP,列出方程即可解决问题;
【考点精析】掌握平行线分线段成比例是解答本题的根本,需要知道三条平行线截两条直线,所得的对应线段成比例.

【题目】九 (1)班48名学生参加学校举行的“珍惜生命,远离毒品”只是竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下8名学生成绩尚未统计,这8名学生成绩如下:60,90,63,99,67,99,99,68. 频数分布表
分数段 | 频数(人数) |
60≤x<70 | a |
70≤x<80 | 16 |
80≤x<90 | 24 |
90≤x<100 | b |

请解答下列问题:
(1)完成频数分布表,a= , b= .
(2)补全频数分布直方图;
(3)全校共有600名学生参加初赛,估计该校成绩90≤x<100范围内的学生有多少人?
(4)九 (1)班甲、乙、丙三位同学的成绩并列第一,现选两人参加决赛,求恰好选中甲、乙两位同学的概率.