题目内容
【题目】如图,直角梯形ABCO的两边OA,OC在坐标轴的正半轴上,BC∥x轴,OA=OC=4,以直线x=1为对称轴的抛物线过A,B,C三点.
(1)求该抛物线的函数解析式;
(2)已知直线![]() 的解析式为y=x+m,它与x轴交于点G,在梯形ABCO的一边上取点P.
的解析式为y=x+m,它与x轴交于点G,在梯形ABCO的一边上取点P.
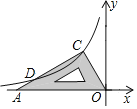
①当m=0时,如图1,点P是抛物线对称轴与BC的交点,过点P作PH⊥直线![]() 于点H,连结OP,试求△OPH的面积;
于点H,连结OP,试求△OPH的面积;
②当m=﹣3时,过点P分别作x轴、直线![]() 的垂线,垂足为点E,F.是否在线段BC存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
的垂线,垂足为点E,F.是否在线段BC存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.

【答案】(1)![]() (2)①
(2)①![]() ②存在满足条件的点P,点P坐标为:(7﹣4
②存在满足条件的点P,点P坐标为:(7﹣4![]() ,4)
,4)
【解析】
试题(1)利用待定系数法求出抛物线的解析式;(2)①如答图1,作辅助线,利用关系式S△OPH=S△OMH-S△OMP求解;②本问涉及复杂的分类讨论,如答图2所示.由于点P可能在OC、BC、BK、AK、OA上,而等腰三角形本身又有三种情形,故讨论与计算的过程比较复杂,需要耐心细致、考虑全面.
试题解析:(1)由题意得:A(4,0),C(0,4),对称轴为x=1.
设抛物线的解析式为y=ax2+bx+c,则有:
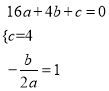 , 解得
, 解得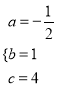 .
.
∴抛物线的函数解析式为:![]()
(2)①当m=0时,直线![]() :y=x.
:y=x.
∵抛物线对称轴为x=1,
∴CP=1.
如答图1,延长HP交y轴于点M,则△OMH、△CMP均为等腰直角三角形.
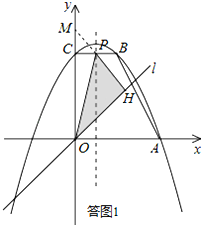
∴CM=CP=1,
∴OM=OC+CM=5.
S△OPH=S△OMH﹣S△OMP=![]() (
(![]() OM)2﹣
OM)2﹣![]() OMCP=
OMCP=![]() ×(
×(![]() ×5)2﹣
×5)2﹣![]() ×5×1=
×5×1=![]() ﹣
﹣![]() =
=![]() ,
,
∴S△OPH=![]() .
.
②当m=﹣3时,直线l:y=x﹣3.
设直线![]() 与x轴、y轴交于点G、点D,则G(3,0),D(0,﹣3).
与x轴、y轴交于点G、点D,则G(3,0),D(0,﹣3).
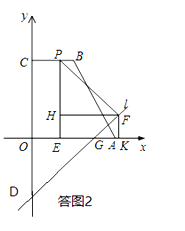
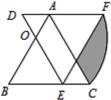
假设存在满足条件的点P.如答图2所示,此时PE=4.
若PE=PF,则点P为∠OGD的角平分线与BC的交点,有GE=GF,过点F分别作FH⊥PE于点H,FK⊥x轴于点K,
∵∠OGD=135°,
∴∠EPF=45°,即△PHF为等腰直角三角形,
设GE=GF=t,则GK=FK=EH=![]() t,
t,
∴PH=HF=EK=EG+GK=t+![]() t,
t,
∴PE=PH+EH=t+![]() t+
t+![]() t=4,
t=4,
解得t=4![]() ﹣4,则OE=3﹣t=7﹣4
﹣4,则OE=3﹣t=7﹣4![]() ,
,
∴P2(7﹣4![]() ,4)
,4)
另外,PE=EF,EF=PF不可能.
综上所述,存在满足条件的点P,点P坐标为:(7﹣4![]() ,4).
,4).

综上所述,存在满足条件的点P,点P坐标为:(7﹣4![]() ,4)
,4)