题目内容
【题目】一位小朋友在粗糙不打滑的“Z”字形平面轨道上滚动一个半径为10cm的圆盘,如图所示,AB与CD是水平的,BC与水平面的夹角为60°,其中AB=60cm,CD=40cm,BC=40cm,那么该小朋友将圆盘从A点滚动到D点其圆心所经过的路线长为___________cm

【答案】![]()
【解析】试题解析:如下图,画出圆盘滚动过程中圆心移动路线的分解图象.
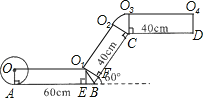
可以得出圆盘滚动过程中圆心走过的路线由线段OO1,线段O1O2,圆弧![]() ,线段O3O4四部分构成.
,线段O3O4四部分构成.
其中O1E⊥AB,O1F⊥BC,O2C⊥BC,O3C⊥CD,O4D⊥CD.
∵BC与AB延长线的夹角为60°,O1是圆盘在AB上滚动到与BC相切时的圆心位置,
∴此时⊙O1与AB和BC都相切.
则∠O1BE=∠O1BF=60度.
此时Rt△O1BE和Rt△O1BF全等,
在Rt△O1BE中,BE=![]() cm.
cm.
∴OO1=AB-BE=(60-![]() )cm.
)cm.
∵BF=BE=![]() cm,
cm,
∴O1O2=BC-BF=(40-![]() )cm.
)cm.
∵AB∥CD,BC与水平夹角为60°,
∴∠BCD=120度.
又∵∠O2CB=∠O3CD=90°,
∴∠O2CO3=60度.
则圆盘在C点处滚动,其圆心所经过的路线为圆心角为60°且半径为10cm的圆弧![]() .
.
∴![]() 的长=
的长=![]() ×2π×10=
×2π×10=![]() πcm.
πcm.
∵四边形O3O4DC是矩形,
∴O3O4=CD=40cm.
综上所述,圆盘从A点滚动到D点,其圆心经过的路线长度是:
(60-![]() )+(40-
)+(40-![]() )+
)+![]() π+40=(140-
π+40=(140-![]() +
+![]() π)cm.
π)cm.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目