题目内容
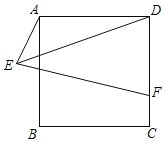
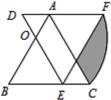
【题目】△ABC为等边三角形,点O为AB边上一点,且BO=2AO=4,将△ABC绕点O逆时针旋转60°得△DEF,则图中阴影部分的面积为______.
【答案】![]()
【解析】
连接OC,OF,作CG⊥AB,OM⊥BC, FH⊥AB的延长线于点H.根据三线合一求出BG= AG=3,进而求得OG,由三角函数求得CG,解直角三角形OGC得出OC长,再由面积公式分别求得![]() ,
,![]() =
=![]() ,
,![]() ,
,![]() ,利用
,利用![]() =
=![]() +
+ ![]() +
+![]() -
-![]() -
-![]() 求得答案即可.
求得答案即可.
连接OC,OF,作CG⊥AB,OM⊥BC, FH⊥AB的延长线于点H.
∵BO=2AO=4,
∴AO=2,AB=6,
∵△ABC为等边三角形,CG⊥AB,
∴BG= AG=![]() AB=3,CG=BC·sin60°=
AB=3,CG=BC·sin60°= ![]() ,
,
∴OG=3-2=1,
Rt△OGC中,OG=1,CG=![]() ,
,
∴OC=![]() =
=![]() ,
,
易证△NEC,△AOD,△BOE为等边三角形,四边形AOEF为等腰梯形,
∴AF=OE=4,CE=AO=2,OM=HF=4×sin60°=![]() ,
,

∵′![]() =
=  =
= ![]() ,
, ![]() =
=![]() =
= ![]() =
= ![]() ,
,
![]() =
= ![]() =
= ![]() ,
, ![]() =
= ![]() =
= ![]() ,
,
∴![]() =
=![]() +
+ ![]() +
+![]() -
-![]() -
-![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目