题目内容
【题目】（1）（发现证明）
如图1，在正方形ABCD中，点E，F分别是BC，CD边上的动点，且∠EAF＝45°，求证：EF＝DF+BE．
小明发现，当把△ABE绕点A顺时针旋转90°至△ADG，使AB与AD重合时能够证明，请你给出证明过程．
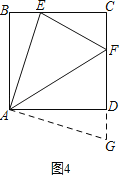
（2）（类比引申）①如图2，在正方形ABCD中，如果点E，F分别是CB，DC延长线上的动点，且∠EAF＝45°，则（1）中的结论还成立吗？请写出证明过程．
②如图3，如果点E，F分别是BC，CD延长线上的动点，且∠EAF＝45°，则EF，BE，DF之间的数量关系是 （不要求证明）
（3）（联想拓展）如图1，若正方形ABCD的边长为6，AE＝3
，求AF的长．
【答案】（1）证明见解析；（2）①不成立，结论：EF＝DF﹣BE；证明见解析；②BE＝EF+DF；（3）AF＝
．
【解析】
（1）【发现证明】
证明△EAF≌△GAF，可得出EF＝FG，则结论得证；
（2）【类比引申】
①将△ABE绕点A顺时针旋转90°至△ADM根据SAS可证明△EAF≌△MAF，可得EF＝FM，则结论得证；
②将△ADF绕点A逆时针旋转90°至△ABN，证明△AFE≌△ANE，可得出EF＝EN，则结论得证；
（3）【联想拓展】
求出DG＝2，设DF＝x，则EF＝DG＝x+3，CF＝6﹣x，在Rt△EFC中，得出关于x的方程，解出x则可得解．
（1）【发现证明】
证明：把△ABE绕点A顺时针旋转90°至△ADG，如图1，
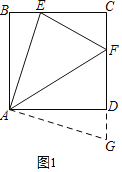
∴∠BAE＝∠DAG，AE＝AG，
∵∠EAF＝45°，
∴∠BAE+∠FAD＝45°，
∴∠DAG+∠FAD＝45°，
∴∠EAF＝∠FAG，
∵AF＝AF，
∴△EAF≌△GAF（SAS），
∴EF＝FG＝DF+DG，
∴EF＝DF+BE；
（2）【类比引申】
①不成立，结论：EF＝DF﹣BE；
证明：如图2，将△ABE绕点A顺时针旋转90°至△ADM，
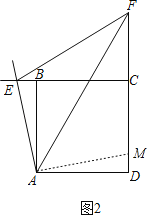
∴∠EAB＝∠MAD，AE＝AM，∠EAM＝90°，BE＝DM，
∴∠FAM＝45°＝∠EAF，
∵AF＝AF，
∴△EAF≌△MAF（SAS），
∴EF＝FM＝DF﹣DM＝DF﹣BE；
②如图3，将△ADF绕点A逆时针旋转90°至△ABN，
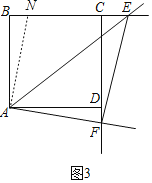
∴AN＝AF，∠NAF＝90°，
∵∠EAF＝45°，
∴∠NAE＝45°，
∴∠NAE＝∠FAE，
∵AE＝AE，
∴△AFE≌△ANE（SAS），
∴EF＝EN，
∴BE＝BN+NE＝DF+EF．
即BE＝EF+DF．
故答案为：BE＝EF+DF．
（3）【联想拓展】
解：由（1）可知AE＝AG＝3
，
∵正方形ABCD的边长为6，
∴DC＝BC＝AD＝6，
∴
＝
＝3．
∴BE＝DG＝3，
∴CE＝BC﹣BE＝6﹣3＝3，
设DF＝x，则EF＝DG＝x+3，CF＝6﹣x，
在Rt△EFC中，∵CF2+CE2＝EF2，
∴（6﹣x）2+32＝（x+3）2，
解得：x＝2．
∴DF＝2，
∴AF＝
＝
＝2
．
