题目内容
【题目】某工厂设计了一款成本为20元/件的工艺品投放市场进行试销，经过调查，得到如下数据：
销售单价 | … | 30 | 40 | 50 | 60 | … |
每天销售量 | … | 500 | 400 | 300 | 200 | … |
（1）研究发现，每天销售量
与单价
满足一次函数关系，求出与的关系式；
（2）当地物价部门规定，该工艺品销售单价最高不能超过45元/件，那么销售单价定为多少时，工艺厂试销该工艺品每天获得的利润8000元？
【答案】（1）y＝﹣10x+800；（2）单价定为40元/件时，工艺厂试销该工艺品每天获得的利润8000元
【解析】
（1）直接利用待定系数法求解可得；
（2）根据“总利润
单件利润
销售量”可得关于
的一元二次方程，解之即可得．
解：（1）设y＝kx+b，
根据题意可得
，
解得：
，
每天销售量
与单价的函数关系为：y＝﹣10x+800，
（2）根据题意，得：（x﹣20）（﹣10x+800）＝8000，
整理，得：x2﹣100x+2400＝0，解得：x1＝40，x2＝60，
∵销售单价最高不能超过45元/件，
∴x＝40，
答：销售单价定为40元/件时，工艺厂试销该工艺品每天获得的利润8000元.
【题目】距离中考体育考试时间越来越近，某校想了解初三年级1500名学生跳绳情况，从中随机抽查了20名男生和20名女生的跳绳成绩，收集到了以下数据：
男生：192、166，189，186，184，182，178，177，174，170，188，168，205，165，158，150，188，172，180，188
女生：186，198，162，192，188，186，185，184，180，180，186，193，178，175，172，166，155，183，187，184．
根据统计数据制作了如下统计表：
个数x | 150≤x＜170 | 170≤x＜185 | 185≤x＜190 | x≥190 |
男生 | 5 | 8 | 5 | 2 |
女生 | 3 | 8 | a | 3 |
两组数据的极差、平均数、中位数、众数如表所示：
极差 | 平均数 | 中位数 | 众数 | |
男生 | 55 | 178 | b | c |
女生 | 43 | 181 | 184 | 186 |
（1）请将上面两个表格补充完整：a＝____，b＝_____，c＝_____；
（2）请根据抽样调查的数据估计该校初三年级学生中考跳绳成绩能得满分（185个及以上）的同学大约能有多少人？
（3）体育组的江老师看了表格数据后认为初三年级的女生跳绳成绩比男生好，请你结合统计数据，写出支持江老师观点的理由．
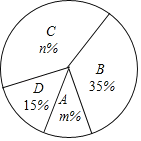
【题目】今年5月份，我市某中学开展争做“五好小公民”征文比赛活动，赛后随机抽取了部分参赛学生的成绩，按得分划分为A，B，C，D四个等级，并绘制了如下不完整的频数分布表和扇形统计图：
等级 | 成绩（s） | 频数（人数） |
A | 90＜s≤100 | 4 |
B | 80＜s≤90 | x |
C | 70＜s≤80 | 16 |
D | s≤70 | 6 |
根据以上信息，解答以下问题：
（1）表中的x= ；
（2）扇形统计图中m= ，n= ，C等级对应的扇形的圆心角为 度；
（3）该校准备从上述获得A等级的四名学生中选取两人做为学校“五好小公民”志愿者，已知这四人中有两名男生（用a1，a2表示）和两名女生（用b1，b2表示），请用列表或画树状图的方法求恰好选取的是a1和b1的概率．
