Question

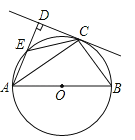
【题目】如图，AB为⊙O的直径，C为⊙O上一点，AD与过点C的切线互相垂直，垂足为点D，AD交⊙O于点E，连接CE，CB．

（1）求证：CE=CB；

（2）若AC=，CE=，求AE的长．

Answer 1

【答案】（1）证明见解析；（2）3．

【解析】

试题分析：（1）连接OC，利用切线的性质和已知条件推知OC∥AD，根据平行线的性质和等角对等边证得结论；

（2）AE=AD﹣ED，通过相似三角形△ADC∽△ACB的对应边成比例求得AD=4，DC=2．在直角△DCE中，由勾股定理得到DE==1，故AE=AD﹣ED=3．

试题解析：（1）证明：连接OC，∵CD是⊙O的切线，∴OC⊥CD．

∵AD⊥CD，∴OC∥AD，∴∠1=∠3．

又OA=OC，∴∠2=∠3，∴∠1=∠2，∴CE=CB；

（2）解：∵AB是直径，∴∠ACB=90°，∵AC=，CB=CE=，∴AB= = =5．∵∠ADC=∠ACB=90°，∠1=∠2，∴△ADC∽△ACB，∴，即，∴AD=4，DC=2．在直角△DCE中，DE==1，∴AE=AD﹣ED=4﹣1=3．