题目内容
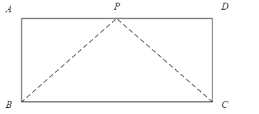
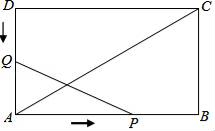
【题目】如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动,点Q沿DA边从点D开始向点A以1cm/s的速度移动,如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤6),那么:
(1)当t为何值时,△QAP是等腰直角三角形?
(2)当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似?
【答案】(1)当t=2s时,△QAP为等腰直角三角形;(2)①当t=1.2s时,△QAP∽△ABC;②当t=1.2s或3s时,以点Q、A、P为顶点的三角形与△ABC相似.
【解析】试题分析:(1)根据等腰三角形的性质可得QA=AP,从而可以求得结果;
(2)分![]() 与
与![]() 两种情况结合相似三角形的性质讨论即可.
两种情况结合相似三角形的性质讨论即可.
(1)由QA=AP,即6-t="2t" 得t="2" (秒);
(2)当![]() 时,△QAP~△ABC,则
时,△QAP~△ABC,则![]() ,解得t=1.2(秒)
,解得t=1.2(秒)
当![]() 时,△QAP~△ABC,则
时,△QAP~△ABC,则![]() ,解得t=3(秒)
,解得t=3(秒)
∴当t=1.2或3时,△QAP~△ABC.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目