题目内容
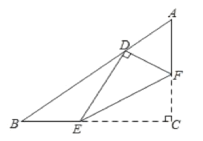
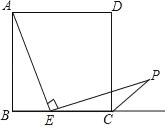
【题目】如图，在边长为3的正方形ABCD中，点E是BC边上的点，EC=2，∠AEP=90°，且EP交正方形外角的平分线CP于点P，则PC的长为_____．
【答案】
【解析】
在AB上取BN=BE，连接EN，根据已知及正方形的性质利用ASA判定△ANE≌△ECP，从而得到NE=CP，在等腰直角三角形BNE中，由勾股定理即可解决问题．
在AB上取BN=BE，连接EN，作PM⊥BC于M．
∵四边形ABCD是正方形，∴AB=BC，∠B=∠DCB=∠DCM=90°．
∵BE=BN，∠B=90°，∴∠BNE=45°，∠ANE=135°．
∵PC平分∠DCM，∴∠PCM=45°，∴∠ECP=135°．
∵AB=BC，BN=BE，∴AN=EC．
∵∠AEP=90°，∴∠AEB+∠PEC=90°．
∵∠AEB+∠NAE=90°，∴∠NAE=∠PEC，∴△ANE≌△ECP（ASA），∴NE=CP．
∵BC=3，EC=2，∴NB=BE=1，∴NE=
=，∴PC=．
故答案为：．
练习册系列答案
相关题目
