ЬтФПФкШн
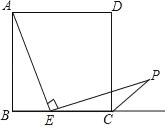
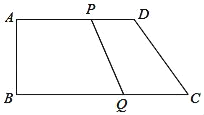
ЁОЬтФПЁПШчЭМЃЌдкдкЫФБпаЮABCDжаЃЌADЁЮBCЃЌЁЯBЃН90ЁуЃЌЧвADЃН12cmЃЌABЃН8cmЃЌDCЃН10cmЃЌШєЖЏЕуPДгAЕуГіЗЂЃЌвдУПУы2cmЕФЫйЖШбиЯпЖЮADЯђЕуDдЫЖЏЃЛЖЏЕуQДгCЕуГіЗЂвдУПУы3cmЕФЫйЖШбиCBЯђBЕудЫЖЏЃЌЕБPЕуЕНДяDЕуЪБЃЌЖЏЕуPЁЂQЭЌЪБЭЃжЙдЫЖЏЃЌЩшЕуPЁЂQЭЌЪБГіЗЂЃЌВЂдЫЖЏСЫtУыЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉBCЃНЁЁ ЁЁcmЃЛ
ЃЈ2ЃЉЕБtЃНЁЁ ЁЁУыЪБЃЌЫФБпаЮPQBAГЩЮЊОиаЮЃЎ
ЃЈ3ЃЉЪЧЗёДцдкtЃЌЪЙЕУЁїDQCЪЧЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ18ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉДцдкtЃЌЪЙЕУЁїDQCЪЧЕШбќШ§НЧаЮЃЌДЫЪБtЕФжЕЮЊ
ЃЛЃЈ3ЃЉДцдкtЃЌЪЙЕУЁїDQCЪЧЕШбќШ§НЧаЮЃЌДЫЪБtЕФжЕЮЊ![]() УыЛђ4УыЛђ
УыЛђ4УыЛђ![]() УыЃЎ
УыЃЎ
ЁОНтЮіЁП
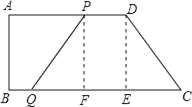
ЃЈ1ЃЉзїDEЁЭBCгкEЃЌдђЫФБпаЮABEDЮЊОиаЮЃЎдкжБНЧЁїCDEжаЃЌвбжЊDCЁЂDEЕФГЄЃЌИљОнЙДЙЩЖЈРэПЩвдМЦЫуECЕФГЄЖШЃЌИљОнBCЃНBE+ECМДПЩЧѓГіBCЕФГЄЖШЃЛ
ЃЈ2ЃЉЕБPAЃНBQЪБЃЌЫФБпаЮPQBAЮЊОиаЮЃЌИљОнPAЃНQBСаГіЙигкtЕФЗНГЬЃЌНтЗНГЬМДПЩЃЛ
ЃЈ3ЃЉвђЮЊШ§БпжаЃЌУПСНЬѕБпЖМгаЯрЕШЕФПЩФмЃЌЫљвдгІПМТЧШ§жжЧщПіЃЎНсКЯТЗГЬЃНЫйЖШЁСЪБМфЧѓЕУЦфжаЕФгаЙиЕФБпЃЌдЫгУЕШбќШ§НЧаЮЕФаджЪКЭНтжБНЧШ§НЧаЮЕФжЊЪЖЧѓНтЃЎ
НтЃКИљОнЬтвтЕУЃКPAЃН2tЃЌCQЃН3tЃЌдђPDЃНADЉPAЃН12Љ2tЃЌ
ЃЈ1ЃЉШчЭМЃЌЙ§DЕузїDEЁЭBCгкEЃЌдђЫФБпаЮABEDЮЊОиаЮЃЌDEЃНABЃН8cmЃЌADЃНBEЃН12cmЃЌ
дкжБНЧЁїCDEжаЃЌЁпЁЯCEDЃН90ЁуЃЌDCЃН10cmЃЌDEЃН8cmЃЌ
ЁрECЃН![]() ЃН6cmЃЌ
ЃН6cmЃЌ
ЁрBCЃНBE+ECЃН18cmЃЎ
ЙЪД№АИЮЊ18ЃЛ
ЃЈ2ЃЉЁпADЁЮBCЃЌЁЯBЃН90Ёу
ЁрЕБPAЃНBQЪБЃЌЫФБпаЮPQBAЮЊОиаЮЃЌ
МД2tЃН18Љ3tЃЌ
НтЕУtЃН![]() УыЃЌ
УыЃЌ
ЙЪЕБtЃН![]() УыЪБЫФБпаЮPQBAЮЊОиаЮЃЛ
УыЪБЫФБпаЮPQBAЮЊОиаЮЃЛ
ЙЪД№АИЮЊ![]()
ЃЈ3ЃЉЁїDQCЪЧЕШбќШ§НЧаЮЪБЃЌЗжШ§жжЧщПіЬжТлЃК
ЂйЕБQCЃНDCЪБЃЌМД3tЃН10ЃЌ
ЁрtЃН![]() ЃЛ
ЃЛ
ЂкЕБDQЃНDCЪБЃЌ![]() ЃН6ЃЌ
ЃН6ЃЌ
ЁрtЃН4ЃЛ
ЂлЕБQDЃНQCЪБЃЌ3t![]() ЃН5ЃЌ
ЃН5ЃЌ
ЁрtЃН![]() ЃЎ
ЃЎ
ЙЪДцдкtЃЌЪЙЕУЁїDQCЪЧЕШбќШ§НЧаЮЃЌДЫЪБtЕФжЕЮЊ![]() УыЛђ4УыЛђ
УыЛђ4УыЛђ![]() УыЃЎ
УыЃЎ

 НђЧХНЬг§МЦЫуаЁзДдЊЯЕСаД№АИ
НђЧХНЬг§МЦЫуаЁзДдЊЯЕСаД№АИ