题目内容
【题目】我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.

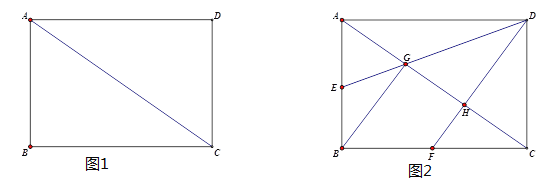
(1)已知:如图1,四边形ABCD是等对角四边形,∠A≠∠C,∠A=60°,∠B=75°,则:∠C= °,∠D= °;
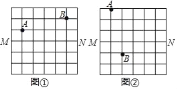
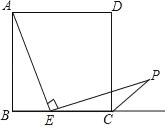
(2)已知,如图2,在平面直角坐标系xOy中,四边形ABCD是等对角四边形,其中A(﹣2,0),C(2,0),B(-1,![]() ),点D在y轴上.
),点D在y轴上.
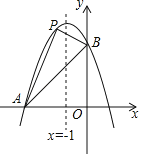
①若抛物线y=ax2+bx+c过点A,C,D,求二次函数的解析式;
②若抛物线y=ax2+bx+c(a<0)过点A,C,点P在抛物线上,当满足∠APC=![]() ∠ADC的P点至少有3个时,总有不等式2n﹣
∠ADC的P点至少有3个时,总有不等式2n﹣![]()
![]() +
+![]() 成立,求n的取值范围.
成立,求n的取值范围.
【答案】(1)150,75;(2)①y=﹣![]() x2+2;②n≤
x2+2;②n≤![]() .
.
【解析】
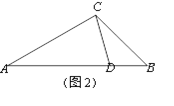
(1)∠A≠∠C,∠A=60°,∠B=75°,则∠B=75°=∠D,四边形的内角和为360°,故∠C=150°,即可求解;
(2)①证明△ACD为等腰直角三角形,故点D(0,2),即可求解;
②以D(0,2)为圆心,AD长为半径作⊙D,以D’(0,-2)为圆心,AD长为半径作⊙D’,如图所示,⊙D交y轴正半轴于点E,⊙D′交y轴负半轴于点F,当点P在优弧AEC和优弧AFC上时,∠APC=![]() ∠ADC,当抛物线过E点时满足题意的P点有3个,即可求解.
∠ADC,当抛物线过E点时满足题意的P点有3个,即可求解.
(1)∠A≠∠C,∠A=60°,∠B=75°,则∠B=75°=∠D,
四边形的内角和为360°,故∠C=150°,
故答案为:150,75;
(2)①如图2,过点B作BH⊥x轴于点H,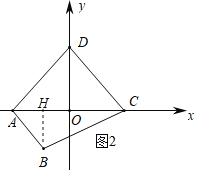
则AH=OH=1,BH=![]() ,HC=3,
,HC=3,
故tan∠HAB=![]() =tan∠HBC,
=tan∠HBC,
则∠BAH=∠CHB=60°,∴∠ABC=90°,
而∠DAO=∠DCO,∠CAB=60°,∠BCA=30°,
∴∠DAB≠∠DCB,故∠ADC=∠ABC=90°,
故△ACD为等腰直角三角形,故点D(0,2),
则抛物线的表达式为:y=ax2+2,
将点A的坐标代入上式并解得:a=-![]() ,
,
故抛物线的表达式为:y=-![]() x2+2;
x2+2;
②∵A(-2,0)、C(2,0)、B(-1,-![]() ),
),
∴AB=2,BC=2![]() ,AC=4,
,AC=4,
∴AB2+BC2=AC2,∴∠ABC=90°,
∵AD=CD,AB≠BC,
∴∠BAD≠∠BCD,
∵四边形ABCD是“等对角四边形”
∴∠ADC=∠ABC=90°,∴D(0,2)
∵抛物线y=ax2+bx+c过点A、C,
∴y=a(x+2)(x-2)=ax2-4a,
即:a=-![]() c,令t=2c2+16a-8
c,令t=2c2+16a-8![]() ,
,
则t=2c2-4c-8![]() ,
,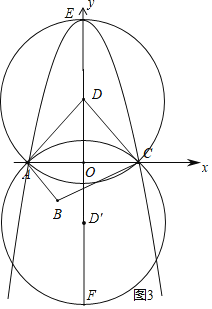
以D(0,2)为圆心,AD长为半径作⊙D,以D′(0,-2)为圆心,AD长为半径作⊙D′,
如图所示,⊙D交y轴正半轴于点E,⊙D′交y轴负半轴于点F.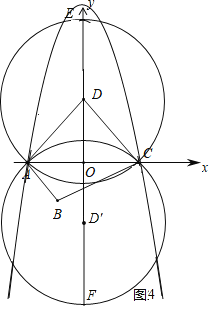
当点P在优弧AEC和优弧AFC上时,∠APC=![]() ∠ADC,当抛物线过E点时满足题意的P点有3个,
∠ADC,当抛物线过E点时满足题意的P点有3个,
此时,c=OE=OD+ED=2+2![]() ,
,
当满足∠APC=![]() ∠ADC的P点至少有3个时,c≥2+2
∠ADC的P点至少有3个时,c≥2+2![]() ,
,
当c≥2+2![]() 时,t=2c2-4c-8
时,t=2c2-4c-8![]() ≥16,
≥16,
∵总有不等式2n-![]() ≤2c2+16a-8
≤2c2+16a-8![]() 成立
成立
∴2n-![]() ≤16,
≤16,
解得:n≤![]() .
.