题目内容
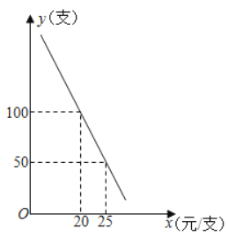
【题目】在2019年某中学举行的冬季阳径运动会上，参加男子跳高的15名运动员的成绩如表所示：
成绩（m） | 1.80 | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 |
人数 | 1 | 2 | 4 | 3 | 3 | 2 |
这些运动员跳高成绩的中位数和众数分别是（ ）
A.
B.
C.
D.
【答案】D
【解析】
首先根据这组数据的个数是奇数，则处于中间位置的数就是这组数据的中位数，判断出这些运动员跳高成绩的中位数即可；然后找出这组数据中出现次数最多的数，则它就是这些运动员跳高成绩的众数，据此解答即可．
解：∵15÷2＝7…1，第8名的成绩处于中间位置，
∴男子跳高的15名运动员的成绩处于中间位置的数是1.65m，
∴这些运动员跳高成绩的中位数是1.65m；
∵男子跳高的15名运动员的成绩出现次数最多的是1.60m，
∴这些运动员跳高成绩的众数是1.60m；
综上，可得这些运动员跳高成绩的中位数是1.65m，众数是1.60m．
故选：D．
练习册系列答案
相关题目
【题目】小云在学习过程中遇到一个函数
．下面是小云对其探究的过程，请补充完整：
（1）当
时，对于函数
，即
，当时，
随
的增大而 ，且
；对于函数
，当时，
随的增大而 ，且
；结合上述分析，进一步探究发现，对于函数
，当时，随的增大而 ．
（2）当
时，对于函数，当时，与的几组对应值如下表：
| 0 |
| 1 |
| 2 |
| 3 |
|
| 0 |
|
|
| 1 |
|
|
|
综合上表，进一步探究发现，当时，随的增大而增大．在平面直角坐标系
中，画出当时的函数的图象．
（3）过点(0，m)（
）作平行于轴的直线
，结合（1）（2）的分析，解决问题：若直线与函数的图象有两个交点，则
的最大值是 ．
