题目内容
【题目】（模型建立）
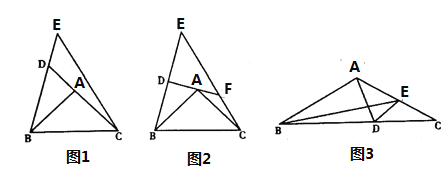
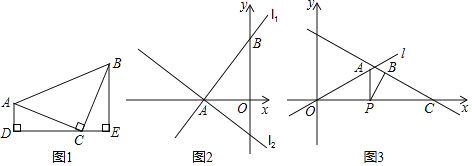
（1）如图1，等腰直角三角形ABC中，∠ACB＝90°，CA＝CB，直线ED经过点C，过A作AD⊥ED于点D，过B作BE⊥ED于点E．
求证：△CDA≌△BEC．
（模型运用）
（2）如图2，直线l1：y＝
x+4与坐标轴交于点A、B，将直线l1绕点A逆时针旋转90°至直线l2，求直线l2的函数表达式．
（模型迁移）
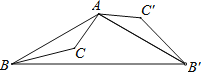
如图3，直线l经过坐标原点O，且与x轴正半轴的夹角为30°，点A在直线l上，点P为x轴上一动点，连接AP，将线段AP绕点P顺时针旋转30°得到BP，过点B的直线BC交x轴于点C，∠OCB＝30°，点B到x轴的距离为2，求点P的坐标．
【答案】（1）见解析；（2）
；（3）点P坐标为（4，0）或（﹣4，0）
【解析】
（1）由“AAS”可证△CDA≌△BEC；
（2）如图2，在l2上取D点，使AD＝AB，过D点作DE⊥OA，垂足为E，由（1）可知△BOA≌△AED，可得DE＝OA＝3，AE＝OB＝4，可求点D坐标，由待定系数法可求解析式；
（3）分两种情况讨论，通过证明△OAP≌△CPB，可得OP＝BC＝4，即可求点P坐标．
（1）证明：∵AD⊥DE，BE⊥DE，
∴∠D＝∠E＝90°，
∴∠BCE+∠CBE=90°，
∵∠ACB＝90°，
∴∠ACD+∠BCE=90°，
∴∠ACD=∠CBE，
又CA＝BC，∠D＝∠E＝90°
∴△CDA≌△BEC（AAS）
（2）如图2，在l2上取D点，使AD＝AB，过D点作DE⊥OA，垂足为E
∵直线y＝
x+4与坐标轴交于点A、B，
∴A（﹣3，0），B（0，4），
∴OA＝3，OB＝4，
由（1）得△BOA≌△AED，
∴DE＝OA＝3，AE＝OB＝4，
∴OE＝7，
∴D（﹣7，3）
设l2的解析式为y＝kx+b，
得
解得
∴直线l2的函数表达式为：
（3）若点P在x轴正半轴，如图3，过点B作BE⊥OC，
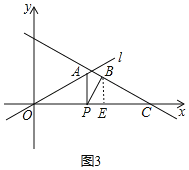
∵BE＝2，∠BCO＝30°，BE⊥OC
∴BC＝4，
∵将线段AP绕点P顺时针旋转30°得到BP，
∴AP＝BP，∠APB＝30°，
∵∠APC＝∠AOC+∠OAP＝∠APB+∠BPC，
∴∠OAP＝∠BPC，且∠OAC＝∠PCB＝30°，AP＝BP，
∴△OAP≌△CPB（AAS）
∴OP＝BC＝4，
∴点P（4，0）
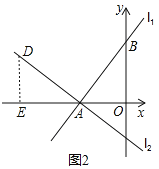
若点P在x轴负半轴，如图4，过点B作BE⊥OC，
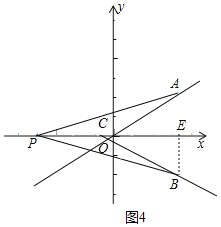
∵BE＝2，∠BCO＝30°，BE⊥OC
∴BC＝4，
∵将线段AP绕点P顺时针旋转30°得到BP，
∴AP＝BP，∠APB＝30°，
∵∠APE+∠BPE＝30°，∠BCE＝30°＝∠BPE+∠PBC，
∴∠APE＝∠PBC，
∵∠AOE＝∠BCO＝30°，
∴∠AOP＝∠BCP＝150°，且∠APE＝∠PBC，PA＝PB
∴△OAP≌△CPB（AAS）
∴OP＝BC＝4，
∴点P（﹣4，0）
综上所述：点P坐标为（4，0）或（﹣4，0）
