题目内容
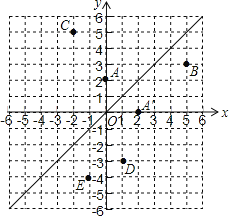
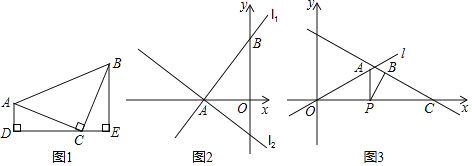
【题目】如图,在6×8的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.
(1)以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′与△ABC位似,且位似比为1:2;(保留作图痕迹,不要求写作法和证明)
(2)若点C的坐标为(2,4),则点A′的坐标为( , ),点C′的坐标为( , ),S△A′B′C′:S△ABC= .
【答案】(1)详见解析;(2)﹣1,0;1,2;1:4.
【解析】
(1)利用△A′B′C′与△ABC位似且位似比为1:2,可将对应点坐标乘以![]() 即可;
即可;
(2)利用所画图形得出对应点坐标后,利用相似三角形的性质求解即可.
解:(1)由图可得A(-2,0),B(4,0),C(2,4),则A’(-1,0),B’(2,0),C’(1,2),
如图所示:△A′B′C′即为所求;
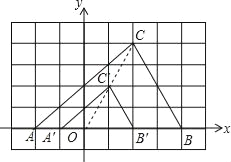
(2)A′(﹣1,0),C′(1,2),
S△A′B′C′:S△ABC=1:4.
故答案为:﹣1,0;1,2;1:4.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目