题目内容
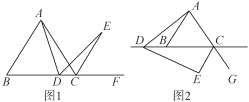
【题目】如图1,△ABC为等边三角形,D为BC上任一点,∠ADE=60°,边DE与∠ACB外角的平分线相交于点E.
(1)求证:AD=DE.
(2)若点D在CB的延长线上,如图2,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.
【答案】(1)证明见解析;(2)成立,证明见解析.
【解析】
(1)在AB上取一点M,使BM=BD,连接MD.则△BDM是等边三角形,则易证AM=DC,根据ASA即可证得△AMD≌△DCE(ASA),根据全等三角形的对应边相等,即可证得;
(2)延长CA到M,使AM=BD,与(1)相同,可证△CDM是等边三角形,然后证明△AMD≌△ECD(ASA),根据全等三角形的对应边相等,即可证得.
(1)证明:如图1,在AB上取一点M,使BM=BD,连接MD.
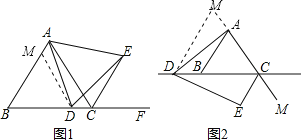
∵△ABC是等边三角形,
∴∠B=60°,BA=BC.
∴△BMD是等边三角形,∠BMD=60°.∠AMD=120°.
∵CE是外角∠ACF的平分线,
∴∠ECF=60°,∠DCE=120°.
∴∠AMD=∠DCE.
∵∠ADE=∠B=60°,∠ADC=∠CDE+∠ADE=∠MAD+∠B,
∴∠CDE=∠MAD.
又∵BA-BM=BC-BD,即MA=CD.
在△AMD和△DCE中,
 ,
,
∴△AMD≌△DCE(ASA),
∴AD=DE.
(2)答:正确.
证明:延长CA到M,使AM=BD,与(1)相同,可证△CDM是等边三角形,
∴∠CDM=∠M=60°,CD=DM,
∵∠ADE=60°,
∴∠ADM=∠EDC,
在△AMD和△DCE中,
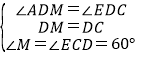 ,
,
∴△AMD≌△ECD(ASA),
∴AD=DE.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目